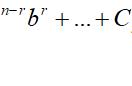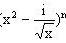由此,我们就可以总结出其系数的变化规律了。
再看前后两项次数的变化规律,a的次数从最大的n变小,每次-1,一直变为0;b的次数从最小的0变大,每次 1,一直变为最大n。
综合起来,我们就可以总结出二项式定理展开式的变化规律了:

并且我们也可以总结出其中各项的通项公式了:

一般,二项式定理考填空题较多,考的就是其展开式的某一项。
考法大致有三种:
(1)普通的两项展开。
例1,若

展开式的常数项为60,则a的数值为?
这样的两项展开,做法就是分次数,把次数分为两个数相加的形式,然后一个给前一项当次数,另一个给后一项当次数,凑出要求的项来。
比如这道例题,需要的是常数项,也就是要让x消失。
所以,要把6分成4 2,其中4给前一项当次数,2给后一项当次数,这样两项相乘正好把x约没了。
再套用二项式定理的通项公式可得,常数项为