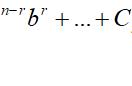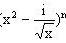二项式中有三项常数项怎么求,二项式三项展开式中的常数项

因此15a=60，解得a=4。

（2）两两相乘的展开。

例2，求

的展开式的常数项是？

像这种两两相乘的，我们先把次数低的那一边展开，再用次数低的展开的每一项去次数高的内寻找对应项，计算出我们需要的项。

这道题就是用前面的两项分别找出可以出现常数项的项。

前一项要去找它的倒数，也就是后面展开式中把5分成1 4，其中1分给前一项当次数，4分给后一项当次数的那一项。

而2本身就是常数项，所以要找后面展开式只有常数项的时候，也就是后面展开式中把5分成0 5，其中0分给前一项当次数，5分给后一项当次数的那一项。

所以，这道题的结果就是

（3）三项展开。

例3，求

的展开式中的常数项为？

像这样三项展开的，我们先把其中两项结合在一起当一项展开一次，然后再把这两项对应的展开一次，找出其中包含我们需要的结果的结合计算在一起即可。

至于先把哪两项结合在一起，其实都可以计算出最后结果，只是会根据题意有计算起来难易的差别，需要大家通过多做题去领悟。

所谓的二项式系数之和就是指前面组合那部分的总和。

所谓的各项系数之和就是把每一项字母前的总系数相加之和。

其规律为：二项式系数之和就看有几项，有几项就是几的n次幂。

比如，计算ax by的n次幂，那么其二项式系数之和就是2的n次幂。

计算ax by cz的n次幂，那么其二项式系数之和就是3的n次幂。

各项系数之和就是把所有的字母全换成1计算出来的最终结果。

比如：计算ax by的n次幂，那么其各项系数之和就是a b的n次幂。

计算ax by cz的n次幂，那么其各项系数之和就是a b c的n次幂。

二项式展开式的所有奇数项系数之和就是把所有字母换成1算出来的数值与把所有字母换成-1算出来的数值之和的一半。

二项式展开式的所有偶数项系数之和就是把所有字母换成1算出来的数值与把所有字母换成-1算出来的数值之差的一半。

以上就是二项式定理的全部内容。

下一节我们讲概率的相关知识点。

大家如果喜欢或者需要这份高中数学学习资料，别忘了点赞关注，我会以最简单明了的方式给大家讲解高中数学，帮助需要的高中生拿个好成绩。