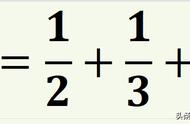怎样找分数里有多少个分数单位,带分数有分数单位吗

分数乘法和分数除法是六年级上册的重点，其中分数乘除法应用题更是必考难点。

解答分数应用题，有一个必要步骤就是寻找分率和分率对应的单位“1”，然后再根据单位“1”是否已知来判断用乘法还是用除法计算。具体解题思路已有总结和例题：

不过不少同学看完之后对于单位“1”还是有一些疑惑，单位“1”到底怎么确定？有没有什么通用的技巧和方法找单位“1”？在这里甜甜老师再梳理一下：

首先弄清楚单位“1”的概念和意义。

单位“1”的概念早在刚开始接触分数的时候就有过介绍。具体在五年级下册分数的意义和性质这一单元中，有明确要求掌握单位“1”和分数的概念和意义。

分数：把单位“1”平均分成若干份，表示其中一份或几份的数，叫做分数。

分数的概念中的单位“1”指的是：一个图形、一个长度单位、一些物体都可以看作一个整体，数学上称这个整体为单位“1”。

举个例子：

1. 图2是把一个长方形平均分成了8格（也就是把这个长方当作单位“1”），涂色的占了其中的5格，用分数表示就是5/8。
2. 图3是把1米平均分成5份（把1米看作单位“1”），涂色的占其中的3份，用分数表示就是3/5。
3. 图4是把6个圆看成一个整体平均分成3份（把6个圆看作单位“1”），涂色的占了2份，用分数表示应该是2/3。

也就是说，把谁平均分，谁就是这个分数的单位“1”。

分率的前面是一个“的”字，谁是谁的几分之几、谁占谁的几分之几、谁相当于谁的几分之几，这类句式一般来说就是分率的前面（“的”字的前面，最靠近分率的这个量）就是单位“1”。例如：

1. 甲数是乙数的4/5。单位“1”：乙数；数量关系：甲数=乙数×4/5；
2. 丙数的3/5等于乙数。单位“1”：丙数；数量关系：丙数×3/5=乙数；
3. 一桶油的3/7是6kg。单位“1”：一桶油的质量；数量关系：一桶油的质量×3/7=6kg；
4. 杨树棵数的5/6相当于柳树棵数。单位“1”：杨树棵树；数量关系：杨树棵树×5/6=柳树棵数。这相当于一个倒转句式，正常的语序应该是柳树棵树是杨树棵数的5/6；
5. 书的价钱正好是钢笔价钱的2/5。单位“1”：钢笔价钱；数量关系：钢笔价钱×2/5=书的价钱；

总结：分率的前面是一个“的”字，那么“的”字前面的那个量就是单位“1”。

如果句式符合“谁是谁的几分之几、谁占谁的几分之几、谁相当于谁的几分之几”这几种句式，那么“是”字的后面、“的”字的前面（“是”字和“的”字之间）就是单位“1”。

这类句式要写数量关系式也非常简单：把“是”字改成“=”，把“的”字改成“×”即可。

这类句式比较灵活，有些分率句会明确说明“谁的几分之几”，如“一本书第一天看了全书的1/8”，这样的句式仍然属于句式一，也就是分率的前面是一个“的”字，“的”字前面的这个量“全书的页数”就是单位“1”。

有些句式就比较隐晦或简单，例如：

1. 某校共有教职工108人，其中男老师占4/9，男老师有多少人。【分率的前面不是“的”字，但是分率句中有一个“其中”，那么“其中”的前面那么总体就是单位“1”。数量关系：全校教职工人数×4/9=男老师人数，也就是108×4/9=48人。】
2. 一本故事书，第一天看了2/5，还剩下144页，这本书一共多少页。【这类句式没有“的”字也没有“其中”，需要根据前后语境来判断。一本故事书，第一天读了“全书的”2/5，把全书页数看作单位“1”。数量关系：全书页数-全书页数×2/5=剩余页数，设全书页数为x接口求解。或者用量率对应：全书页数=144÷（1-2/5）=220页。】
3. 工程队修一条88km的公路，第一周修了3/8，第二周修了余下的3/5，第二周修了多少千米？【这类句式和上一题是一样的，需要根据上下语境来理解，第一周修了“全长的”3/8，第二周修了“余下的”3/5，这两个分率对应的单位“1”是不统一的，第一周以全长为单位“1”，第二周以第一周修完之后剩下的长度为单位“1”。数量关系：全长×3/8=第一周修的长度；（全长-第一周修的长度）×3/5=第二周修的长度，结合在一起就是全长×（1-3/8）×3/5=第二周修的长度=88×5/8×3/5=33千米】

这类句式有一个明显的两个数量的对比，比如：谁比谁多（少）几分之几、今年比去年增产（减产）几分之几、涨价（降价）几分之几。

其规律是两个量做对比，“比”字的后面、“多（少）”字的前面就是单位“1”。可以理解为单位“1”是一个标准量，拿另一个量和它做对比。

涨价和降价比较特殊，一般来说涨价和降价，都是在前一次价格的基础上涨或者降，也就是涨价或降价前最近的那一次价格就是单位“1”。例如：

1. 男生人数比女生多1/5，女生有50人，男生有多少人？【典型的谁比谁多（少）几分之几的句式，“比”字的后面、“的”字的前面 女生人数是单位“1”，男生=女生×（1 1/5）】
2. 一个书包原价100元，现在降价1/10出售，现价多少元？【降价是和原价做对比，在原价的基础上降价，所以原价100元是单位“1”。现价=原价×（1-1/10）=100×（1-1/10）=90元】
3. 一台空调原价4000元，先涨价1/10，然后再降价1/10，现价是多少元。【第一次涨价是在原价4000元的基础上涨，原价是单位“1”，涨价后是4000×（1 1/10）=4400元；第二次降价，是在涨价后的价格上降，也就是4400元是单“1”，所以降价后现价是4400×（1-1/10）=4960元】
4. 某工厂7月份烧煤240吨，比六月份节约了1/9，六月份烧煤多少吨？【“比”字的后面、“节约”的前面 六月份的烧煤量为单位“1”，七月份是跟六月份对比后节约了1/9，数量关系：六月份×（1-1/9）=七月份烧煤量，所以六月份烧煤量=240÷（1-1/9）270吨。】
5. 水凝结成冰体积会增大1/10，那么冰化成水体积会减少几分之几？【这句话要分为2段来理解：水凝结成冰之后体积增大，是和原来水的体积做对比，也就是冰比原来水的体积增大1/10，原来水的体积看作单位“1”，冰的体积=1×（1 1/10）=11/10；然后冰再化成水体积减少，这时是和冰的体积做对比，把冰的体积看作单位“1”，化成水后的体积比冰的体积减少了1/10÷11/10=1/11。】

总结：分率的前面是“多”或者“少”字，也就是谁比谁多（少）几分之几这类句式，“比”字的后面、“多（少）”字的前面就是单位“1”。

同时，“增长、增产、增加、涨价、超额”这类词语的意义相当于“多”，“降低、减产、减少、降价、节约”这类词语的意义相当于“少”。

如果句式不明确，那么就搞清楚是哪两个量在做对比？哪个量作为比较标准？哪个量比哪个量多（少）？被比较的量是比较量，作为比较标准来判断另一个量比他多还是比他少的量是标准量（也就是单位“1”）。

总体来说，当你不熟练的时候，可以把这些规律记住，当你很熟练的时候，学会去分析、理解题目的含义和内在联系，也就不需要这些条条框框了。多练多总结是一个很棒的学习方法。

找准单位“1”之后，基本上分数乘除法应用题就解决了一般。单位“1”是已知量，直接用乘法计算：单位“1”的量×对应分率=分率对应量；单位“1”是未知量、题目要求的量，那就用除法计算：分率对应量÷对应分率=单位“1”的量。

当然遇到数量关系比较复杂的题型的时候，最好画出线段图帮助分析。

本期练习：