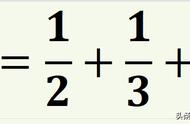一、提炼大概念:
大概念提炼要超越事实性知识和基本技能,上升到概念性理解的水平,形成上位概念,将观点与知识技能联系,迁移才能发生,素养才能形成。本节课大概念的提炼,首先要从分数产生的本源和本质出发思考,为什么要创造分数?分数的本质是什么?如何打通分数与自然数、小数之间的关联,体现数的意义的一致性?
课前慎思:
1、为什么要创造分数?
自然数以1为计数基础,每增加1就形成一个新的数。可是,在分物或测量时,遇到要表达比自然数1更小的数量该怎么办呢?德国数学家克罗内克有一句名言:“上帝创造了自然数,其余都是人造的。”第一个“人为”的数是正分数。整数单位是由小变大,是单位的聚合,是以小量大,直至无限大;小数与分数的计数单位是由大变小,是单位的分解,以大量小,直至无限小。学生之前所经历的计数都是1、0.1、0.01等这样“十进制”的计数单位组成的,而分数的计数则是由1做任意细分而来的,导致学生思维停留在对十进制计数单位度量的认知上而缺乏“任意细分”的意识,无法用“十进制计数单位”的学习方法来同化处理这个新的单位,可这恰恰是一个数感上的反向挑战,正好是“分数单位”得以凸显而感知的机会。
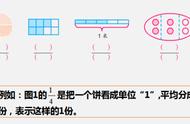
分数借助把“1”平均分成若干份,创造出了分数的计数单位,再计数分数单位的个数,使得用自然数不能计数的量变得可数了,解决了计量比自然数1小的数量的难题。“数起源于数,量起源于量”。从度量的角度引入分数,就与自然数、小数的引入做法一致,能更清楚地体现分数、自然数和小数内在的一致性,把分数置于数的知识体系中,利于建构分数与整数、小数的结构关系。
2、分数的本质是什么?

如何站在单元的整体视角,把握分数的内容结构,抓住分数本质,引导儿童逐步把分数的知识融入数的学习系统,形成知识网络,促进学生的深度学习呢?首先要追根溯源回顾分数产生发展的历史,分析分数本质内涵;其次,要明确分数在数学中的地位及其学习对数学素养的意义和作用;然后,通过多维多元单元整体建构,理解分数本质,建好分数教学的“承重墙”,帮助儿童深刻理解分数的意义;再通过突出整体意识,强化知识深度联系,沟通分数与整数、小数之间的关系,打通数学学习的隔断墙。
依据分数产生的不同路径和发展过程,我们认为分数有以下多个不同的含义:一是分数主要表示“整体与部分之间的关系”或是“两个量之间的关系”,这相当于分数的“比的定义”;二是由“度量”去引入分数,将分数理解为分数单位的累积;三是从“商的定义”引入,表明分数是一种新的数,是两个数相除后所得的结果,能和其他数一样参与运算,为自然数除法运算推向了一个更广阔的视界,这也是分数的本源价值体现;四是将对分数的认识转化为一个运算的过程,也就是“运作”。吴正宪老师的团队指出,在比和数两条主线下,从比率、度量、运算和商四个维度完成对分数意义丰富性的认识。
由此提炼出本节课的大概念:
1、分数是对数量的抽象,1是分数计数的基础,分数借助与1的关系表示比1小的数量,通过1的平均分创造出分数单位,分数单位的累加产生了分数;
2、分数可以表示数量和关系,把一个物体或一个整体看作单位1,通过平均分,借助“份”表示部分和整体或数量和数量之间的关系。
二、转化核心问题:
根据大概念设计本节课的核心问题:
1、为什么要创造分数?怎样表示比1小的数量?
2、分数与自然数、小数之间有什么关系?
3、分数是怎样表达部分与整体的关系的?
三、设计核心任务:
任务一:生活中分物、测量、计算时有没有遇到不到1个的情况,根据已有知识经验,我们是如何解决的?用实物、画图的方式记录你的发现和想法。
追问:
1、我们是怎样数自然数的?自然数中哪个数最为重要?引导汇报:得出1是所有自然数计数的基础,自然数是1的累加。
2、你是怎样表示不到1个的数量的?为什么可以这样表示?通过学生汇报展示,认识单位1,理解不足1个的数量是怎样与1建立联系的?通过对1进行均分,产生份数,不足1的数量与1比较,等于其中几份,从而抽象出分数。
3、分数的产生跟自然数、小数有什么相同的地方?引导汇报;本质相同,都是计数单位累的加。从而突出计数单位的重要性,打通了自然数、分数和小数的关联。
任务二:一个物体可以作为单位1,许多物体可以作单位1吗?你能找到生活中许多物体作单位1的例子吗?摆一摆,画一画,表示出这样的分数?
追问:为什么许多物体也可以作为单位1 ,这样做产生的分数表示什么意义?目的是什么?
引导汇报:用1个物体作单位1,可以表示比1小的数量;用许多物体作单位1,可以表示部分与整体的关系。分数既可以表示数量,也可以表示关系。
四、结构化板书设计: