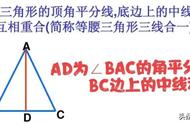
运用等腰三角形 “三线合一” 的性质证明线段相等、角相等或垂直关系,不仅可以减少证全等的次数,而且还可以简化解题过程 .
一、利用 “三线合一” 证明线段相等
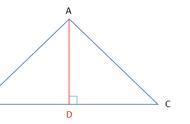
1.如图,已知在 △ABC 中,AB = AC , 点 D,E 在边 BC 上,且 AD = AE .
求证:BD = CE .

证明:过点 A 作 AH⊥BC 于点 H .

∵ AB = AC , AH⊥BC,
∴ BH = CH,
同理可证,DH = EH,
∴ BH - DH = CH - EH ,
∴ BD = CE .
2.如图,在等腰直角 △ABC 中,∠A = 90°,D 为 BC 边上的中点,E,F 分别为 AB , AC 边上的点,
且满足 EA = CF .
求证:DE = DF .

证明:连接 AD .