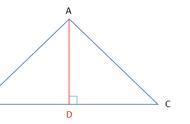
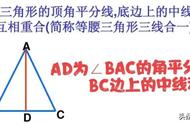
∵ △ABC 为等腰直角三角形,∠BAC = 90°,D 为 BC 边上的中点,
∴ BD = CD = AD , AD 平分 ∠BAC,
∴ ∠EAD = ∠C = 45°,
在 △ADE 和 △CDF 中,
AE = CF , ∠EAD = ∠C,AD = CD .
∴ △ADE ≌ △CDF(SAS),
∴ DE = DF .
二、利用 “三线合一” 证明角相等
3.如图,在 △ABC 中,AB = AC , AD 是 BC 边上的中线,BE⊥AC 于点 E .
求证:∠CBE = ∠BAD .

证明:
∵ AB = AC , AD 是 BC 边上的中线,
∴ AD⊥BC,∠CAD = ∠BAD,
∴ ∠CAD ∠C = 90° .
又 ∵ BE⊥AC,
∴ ∠CBE ∠C = 90°,
∴ ∠CBE = ∠CAD .
∴ ∠CBE = ∠BAD .
4.如图,在 △ACB 中,AC = BC , AD 为 △ABC 的高线,CE 为 △ABC 的中线 .
求证:∠DAB = ∠ACE .

证明:
∵ AC = BC , CE 为 △ABC 的中线,
∴ ∠CAB = ∠B,CE⊥AB,
∴ ∠CAB ∠ACE = 90° .
∵ AD 为 △ABC 的高线,
∴ ∠D = 90°,
∴ ∠DAB ∠B = 90°,
∴ ∠DAB = ∠ACE .
三、利用 “三线合一” 证明垂直关系
5.如图,在 △ABC 中,AC = 2AB , AD 平分 ∠BAC 交 BC 于点 D,E 是 AD 上一点,且 EA = EC .
求证:EB⊥AB .

证明:过点 E 作 EF⊥AC 于点 F .