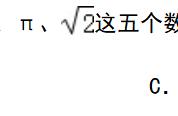一、1.【考点】算术平方根.
【专题】11 :计算题.
【分析】根据算术平方根的定义求解即可求得答案.
【解答】解:∵4的平方=16,
∴16的算术平方根是4.
故选C.
【点评】此题考查了算术平方根的定义.题目很简单,解题要细心.
2.【考点】:在数轴上表示不等式的解集;C6:解一元一次不等式.
【分析】首先解不等式求得不等式的解集,根据数轴上点的表示法即可判断.
【解答】解:解不等式得:x<﹣2.
故选D.
【点评】把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.
3.【考点】:坐标与图形变化﹣平移.
【分析】依据上加下减,右加左边的法则计算即可.
【解答】解:∵1﹣3=﹣2,2﹣1=1.
∴点Q的坐标为(1,﹣2).
故选:C.
【点评】本题主要考查的是坐标与图形的变化,掌握其中的规律是解题的关键.
4.【考点】:全面调查与抽样调查.
【分析】调查方式的选择需要将普查的局限性和抽样调查的必要性结合起来,具体问题具体分析,普查结果准确,所以在要求精确、难度相对不大,实验无破坏性的情况下应选择普查方式,当考查的对象很多或考查会给被调查对象带来损伤破坏,以及考查经费和时间都非常有限时,普查就受到限制,这时就应选择抽样调查.
【解答】解:A、调查具有破坏性,适合抽样调查,故A错误;
B、调查具有破坏性,适合抽样调查,故B错误;
C、了解全班学生的视力情况,故C正确;
D、无法全面调查,故D错误;
故选:C.
【点评】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
5.【考点】:平行线的判定.
【分析】先根据邻补角的定义得到∠3=60°,根据平行线的判定当b与a的夹角为70°时,b∥c,由此得到直线b绕点A逆时针旋转70°﹣60°=10°.
【解答】解:∵∠1=70°,
∴∠3=110°,
∵∠2=120°,
∴当∠3=∠2=120°时,b∥c,
∴直线b绕点A逆时针旋转120°﹣110°=10°.
故选A
【点评】本题考查了平行线的判定:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;两条直线都和第三条直线平行,那么这两条直线平行.
6.【考点】:解一元一次不等式组;点的坐标.
【分析】利用第一象限内点的坐标性质得出关于m的不等式,进而求出即可.
【解答】解:∵点P(m,1﹣m)在第一象限,
∴m>0,1﹣m>0,
解得:0<m<1,
则m的取值范围是:0<m<1.
故选C.
【点评】此题主要考查了点的坐标性质,正确把握各象限内点的坐标性质是解题关键.