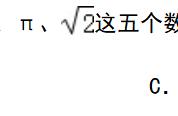解析:利用三角形外角和定理和邻补角的性质求 ∠α 。
∠α = 120° 45° = 165° 或 ∠α = 180° - 15° = 165° 。
例题18、已知:一次函数的图像过点 A(2 ,-2),且与正比例函数的图像相交于点 B(-1 , 4)求此一次函数与正比例函数的解析式。
解:设正比例函数为 y = k1x (k1 ≠ 0), 一次函数为 y = k2x b(k2 ≠ 0)
∵ 正比例函数的图像过点 B(-1 , 4)
∴ 4 = - k1 解得 k1 = -4
∴ 正比例函数的解析式为 y = -4x
又∵ 直线 y = k2x b 过点 A(2 ,-2),(-1 , 4)
∴ 2k2 b = -2 且 -k2 b = 4
∴ k2 = -2 , b =2
∴ 一次函数的解析式为 y = -2x 2
解析:正比例函数与一次函数的一次项系数不一定相同,不能都设为 k 。
例题19、已知一次函数 y = kx 4 (k ≠ 0)的图像与两坐标轴围成的三角形面积为 16 ,求此一次函数的解析式。
解:令 x = 0 , 解得 y = 4 ; 令 y = 0 , 解得 x = -4/k 。
∴ 一次函数 y = kx 4 (k ≠ 0)与 x 轴,y 轴的交点分别是 (0 , 4),(-4/k ,0)
图像与两坐标轴围成的三角形面积是:
1/2 × 4 × ∣-4/k∣ = 16 ,
解得 k = ±1/2
∴ 一次函数的解析式是 y = 1/2 x 4 或 y = -1/2 x 4 。
例题20、如图所示,L1 , L2 分别表示一种白炽灯和一种节能灯的费用 y (费用 = 灯的售价 电费,单位:元)与照明时间 x(小时)的函数图像,假设两种灯的使用寿命都是 2000 小时 ,照明效果一样 。
(1)根据图像分别求出 L1 、L2 的函数表达式;
(2)当照明时间为多少时,两种灯的费用相等?
(3)小明房间计划照明 2500 小时,他买了一个白炽灯和一个节能灯,请你帮他设计最省钱的用灯方法。
(直接给出答案,不必写出解答过程)。

解:
(1)直线 L1 的函数表达式为:y1 = 0.03x 2 (0 ≤ x ≤ 2000 ) ;
直线 L2 的函数表达式为:y2 = 0.012x 20(0 ≤ x ≤ 2000 ) 。
(2)当照明时间为 1000 小时时,两种灯的费用相等 。
(3)先用节能灯 2000 小时,在用白炽灯 500 小时 。