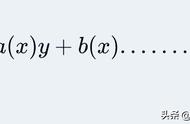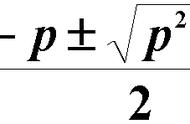的条件,则它是一个全微分方程。对于一个全微分方程,我们可以通过公式来求解其通解。在工程学中,全微分方程的应用非常广泛,因此掌握这个知识点对于学习微积分和应用数学都是非常重要的。

全微分方程作为微积分中的一个重要概念,在物理、工程等领域中也有着广泛的应用。下面以物理学和工程学两个领域作为例子来介绍全微分方程的应用。
物理学中的应用
在物理学中,很多物理现象都可以用微分方程来描述。例如,牛顿第二定律 F=ma 可以转化为运动微分方程 :

其中 m 是物体的质量,x 是物体的位移,t 是时间,F(x) 是作用在物体上的力。如果 F(x) 是一个连续的函数,那么该微分方程是一个全微分方程,我们就可以通过解析的方法来求解它,从而得到物体在空间中的运动轨迹。因此,全微分方程在物理学中有着非常重要的应用。

工程学中的应用
在工程学中,全微分方程也有着广泛的应用。例如,在控制系统设计中,可以用微分方程来描述控制系统的动态特性。如果该微分方程是一个全微分方程,那么我们可以通过解析的方法来求解控制系统的状态响应,从而实现对系统的控制。另外,在电路设计和信号处理中,也可以用微分方程来描述电路和信号的动态特性。如果该微分方程是一个全微分方程,那么我们就可以通过解析的方法来求解电路或信号的响应,从而实现对它们的控制和处理。