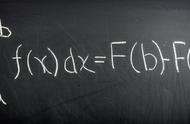微积分是数学中的一门重要分支,它涉及到函数、极限、导数、积分、微分方程等多个概念,在工程、科学、经济等领域都有广泛的应用。微积分分为五个主要的章节:导数与微分、积分与定积分、微分方程与应用、多元函数与偏导数、向量函数与曲线积分。本文将逐一介绍这些内容,以帮助读者了解微积分的基础理论和实际应用。
一、导数与微分导数和微分是微积分理论的基础,它们可以用来描述曲线的变化率、切线斜率以及局部增长和减少的趋势等。导数是函数在某一点的变化率,用极限的概念表示;微分是函数在某一点的切线的近似值,用微分算子的形式表示。导数和微分是密切相关的,在求解导数的同时,也可以求出函数在某一点的微分值。

导数图示
以函数 f(x) = x^2 为例,其导数的计算公式为:

在微积分中,由于极限的存在性,我们可以通过逐步缩小 △x 的值,从而求得 f(x) 在某一点的导数值。此外,微分也是导数的一种几何意义,它表示函数在某一点的切线斜率,可以用于研究函数的局部特征。
二、积分与定积分积分是微积分理论的另一个重要分支,它可以用来计算曲线下方的面积、弧长、体积以及质心等。积分分为不定积分和定积分,其中不定积分表示函数的原函数,而定积分则用于求解函数在一段区间内的积分值。