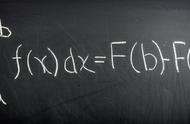以一阶常微分方程 y' y = cos x 为例,其求解过程如下:
首先将方程改写成标准形式: y' = -y cos x ,然后求解其通解:

其中 C 为常数。此外,我们还可以通过初值条件求解微分方程,即通过已知的初始值求解出特定的解。
微分方程的应用十分广泛,例如可以用来描述弹簧振动、电路的变化、生物中的肿瘤扩散、经济模型的预测等。通过求解微分方程的解析解或数值解,我们可以更好地理解各种自然现象和工程问题,并为解决复杂问题提供有效的数学方法。
四、多元函数与偏导数多元函数和偏导数是微积分理论中重要的扩展内容,它们可以用来描述多维空间中的曲面和曲线的性质,以及分析各种复杂问题。在多元函数中,自变量不再是单个变量 x,而是包含多个变量的向量,例如 (x,y,z)。

多元函数图示
以二元函数 z = x^2 y^2 为例,其偏导数的计算公式为:

其中,第一个式子表示 z 对 x 的偏导数,第二个式子表示 z 对 y 的偏导数。偏导数可以用于研究函数在多维空间中的局部性质,例如曲面的切平面、极值点等。
此外,在实际应用中,多元函数和偏导数还可以用于描述电场、磁场、流体力学等复杂现象,在金融领域中也可以利用多元函数和偏导数来进行资产组合优化、风险分析等方面的决策支持。
五、向量函数与曲线积分向量函数和曲线积分是微积分中比较高阶的内容,它们可以用来描述三维空间中的曲线和表面的性质,以及分析各种流体力学、电磁学和物理学问题等。向量函数描述的是在空间中的一个运动路径,其自变量是时间 t 。