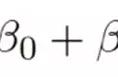简单线性回归也称为一元线性回归,也就是回归模型中只含一个自变量,否则称为多重线性回归。简单线性回归模型为:
Y= a bX ε
式中,Y——因变量;
X——自变量;
a——常数项,是回归直线在纵坐标轴上的截距;
b——回归系数,是回归直线的斜率;
ε——随机误差,即随机因素对因变量所产生的影响。
以“企业季度数据”为例,先撇开其他费用因素,只考虑推广费用对销售额的影响,如果确定了2012年第3季度推广费用预算,通过以上数据,如何预测2012年第3季度销售额呢?
1、绘制散点图
确定好因变量和自变量后,我们需绘制销售额(Y)与推广费用(X1)的散点图。
STEP 01 单击【插入】选项卡【图表】组中的【散点图】,选择【仅带数据标记的散点图】。
STEP 02 弹出一张空白图表,选中该【图表】,单击鼠标右键,在弹出的下拉框中选择【选择数据】。
STEP 03 在弹出的【选择数据源】对话框中,单击【添加】按钮,依次在【X轴序列值(X)】输入“=企业季度数据!C3:C48”,在【Y轴序列值(Y)】输入“=企业季度数据!B3:B48”。
STEP 04 单击【确定】按钮,完成散点图绘制,如图所示。

从这个图中,能够直观地看出推广费用与销售额之间有一定的线性分布特征,我们还可以利用Excel图表工具为其添加趋势线。
STEP 01 选中图表中任一数据点以选中数据系列,单击【布局】选项卡【分析】组中的【趋势线】,选择【其他趋势线选项】。
STEP 02 在弹出的【设置趋势线格式】对话框中,选择【趋势线选项】下的【线性】项,并在对话框下方分别勾选【显示公式】、【显示R平方值】。
STEP 03 单击【确定】按钮,即可得到拟合直线。
拟合曲线方程为:Y=1.198X 4361.5,R2 =0.9055,如图所示。

这只是通过绘图方式建立回归分析模型的一个简单做法,后续还要进一步使用多个统计指标来检验,如回归模型的拟合优度检验(R2)、回归模型的显著性检验(F检验)、回归系数的显著性检验(t检验)等来综合评估回归模型的优劣,这时就需要使用Excel分析工具库中的——“回归”分析工具来实现。
STEP 01 单击【数据】选项卡【分析】组中的【数据分析】按钮,在弹出的【数据分析】对话框中,选择【回归】,单击【确定】按钮。
STEP 02 在弹出【回归】对话框中,对各类参数分别进行如下设置,如图所示。

输入
① Y值输入区域:输入需要分析的因变量数据区域,本例因变量区域为B2:B48。
② X值输入区域:输入需要分析的自变量数据区域,本例自变量区域为C2:C48。
③ 标志:本例勾选【标志】。
④ 常数为零:表示该模型属于严格的正比例模型,因本例不是,故未勾选【常数为零】。
⑤ 置信度:本例勾选此复选框,并输入“95%”。
输出选项
① 输出区域:本例将结果输出至当前工作表的F2单元格。
② 残差:指观测值与预测值(拟合值)之间的差,也称剩余值,本例勾选【残差】。
③ 标准残差:指(残差-残差的均值)/残差的标准差,本例勾选【标准残差】。
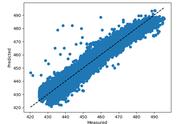
④ 残差图:以回归模型的自变量为横坐标,以残差为纵坐标绘制的散点图。若绘制的点都在以0为横轴的直线上下随机散布,则表示拟合结果合理,否则需要重新建模,本例勾选【残差图】。
⑤ 线性拟合图:以回归模型的自变量为横坐标,以因变量及预测值为纵坐标绘制的散点图,本例勾选【线性拟合图】。
⑥ 正态概率图:以因变量的百分位排名为横坐标,以因变量作为纵坐标绘制的散点图,本例勾选【正态概率图】。
STEP 03 单击【确定】按钮,结果如图所示。

通过Excel分析工具库中的“回归”分析工具,我们可以了解到更多信息,如回归统计表、方差分析表、回归系数表这三张表就分别用于回归模型的拟合优度检验(R2)、回归模型的显著性检验(F检验)、回归系数的显著性检验(t检验)。
2、回归统计表
回归统计表用于衡量因变量Y与自变量X之间相关程度的大小,以及检验样本数据点聚集在回归直线周围的密集程度,从而评价回归模型对样本数据的代表程度,即回归模型的拟合效果,主要包含以下5个部分。
① Multiple R:因变量Y与自变量X之间的相关系数绝对值,本例R=0.9516,销售额与推广费用高度正相关。
② R Square:判定系数R2(也称拟合优度或决定系数),即相关系数R的平方,R2越接近1,表示回归模型拟合效果越好。本例R2=0.9055,回归模型拟合效果好。
③ Adjusted R Square:调整判定系数Adjusted R2,仅用于多重线性回归时才有意义,它用于衡量加入其他自变量后模型的拟合程度。
④ 标准误差:其实应当是剩余标准差(Std. Error of the Estimate),这是Excel中的一个Bug。在对多个回归模型比较拟合程度时,通常会比较剩余标准差,此值越小,说明拟合程度越好,本例剩余标准差为526.41。
⑤ 观测值:用于估计回归模型的数据个数(n),本例n=46。
2、方差分析表
方差分析表的主要作用是通过F检验来判断回归模型的回归效果,即检验因变量与所有自变量之间的线性关系是否显著,用线性模型来描述它们之间的关系是否恰当。表中主要有Df(自由度)、SS(误差平方和)、MS(均方差)、F(F统计量)、Significance F(P值)五大指标,通常我们只需要关注F、Significance F两个指标,其中主要参考Significance F,因为计算出F统计量,还需要查找统计表(F分布临界值表),并与之进行比较才能得出结果,而P值可直接与显著性水平α比较得出结果。
① F:F统计量,用于衡量变量间线性关系是否显著,本例中F=421.54。
② Significance F:是在显著性水平α(常用取值0.01或0.05)下的F的临界值,也就是统计学中常说的P值。一般我们以此来衡量检验结果是否具有显著性,如果P值>0.05,则结果不具有显著的统计学意义;如果0.01<P值≤0.05,则结果具有显著的统计学意义;如果P值≤0.01,则结果具有极其显著的统计学意义。
3、回归系数表
回归系数表主要用于回归模型的描述和回归系数的显著性检验。回归系数的显著性检验,即研究回归模型中的每个自变量与因变量之间是否存在显著的线性关系,也就是研究自变量能否有效地解释因变量的线性变化,它们能否保留在线性回归模型中。
回归系数表(上图左侧第三个表)中,第一列的Intercept、推广费用,分别为回归模型中的a(截距)、b(斜率),对于大多数回归分析来讲,关注b要比a重要;第二列是a和b的值,据此可以写出回归模型;第四、五列分别是回归系数t检验和相应的P值,P值同样与显著性水平α进行比较,最后一列是给出的a和b的95%的置信区间的上下限。
最终我们得到的销售额和推广费用的简单线性回归模型为Y=4361.4864 1.1980X,其中判定系数R2 =0.9055,回归模型拟合效果较好。回归模型的F检验与回归系数的t检验相应的P值都远小于0.01,具有显著线性关系。综合来说,回归模型拟合较好。
我们将制订的2012年第3季度的推广预算值代入回归模型,就可以预测出2012年第3季度的销售额。
,