你是否有过这样的经历,当你看到一组数据时,你会想知道它们之间有没有什么规律?比如,当你看到一些房屋的面积和价格时,你会想知道它们之间有没有什么关系?如果有的话,这个关系是什么样的?能不能用一条直线来描述它们的关系?如果能的话,那么这条直线又能告诉我们什么呢?
这就是线性回归要做的事情。线性回归是一种机器学习算法,它可以用来建立因变量和自变量之间的线性关系模型,从而进行预测或分析 。线性回归的基本思想是,如果两个或多个变量之间存在某种规律,那么我们就可以用一条直线来描述它们的关系,然后根据这条直线来预测未知的变量值。例如,如果我们知道了房屋的面积和价格之间的关系,那么我们就可以用一条直线来表示它们的关系,然后根据这条直线来预测未知面积的房屋价格,或者未知价格的房屋面积。

线性回归的工作过程可以分为两个步骤:训练和预测。
训练:训练就是根据已有的数据集,找到最合适的直线来表示因变量和自变量之间的关系。这个过程需要用到一些数学知识,但我们不在这里展开。简单地说,就是要找到一组参数,使得直线尽可能地贴近数据点,也就是使得误差最小。误差就是真实值和预测值之间的差距。误差越小,说明直线越能反映数据的规律。
预测:预测就是根据训练好的直线,来计算未知变量的值。这个过程很简单,就是把未知变量代入直线方程,然后求出另一个变量的值。例如,如果我们已经知道了房屋面积和价格之间的直线方程是:
Y = 10000 5000 * X
其中,Y 是房价(单位:元),X 是面积(单位:平方米)。那么我们就可以根据这个方程来预测未知面积或价格的值。例如:
如果我们想知道一个100平方米的房子大概多少钱,那么我们就把 X 代入方程,得到:
Y = 10000 5000 * 100 = 510000
也就是说,这个房子大概要51万。
如果我们想知道一个50万的房子大概多大面积,那么我们就把 Y 代入方程,得到:
X = (Y - 10000 ) / 5000 = (500000 - 10000 ) / 5000 = 98
也就是说,这个房子大概有98平方米。
线性回归有哪些应用?线性回归可以用来解决各种实际问题,例如:
1、房价预测:根据房屋的特征(如面积、卧室数量、楼层等)来预测房价。
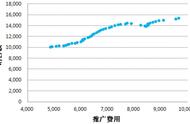
2、广告效果评估:根据广告的投放渠道、时间、内容等因素来评估广告的点击率、转化率等指标。
3、股票预测:根据股票的历史数据(如开盘价、收盘价、成交量等)来预测股票的未来走势。
4、体重控制:根据个人的身高、年龄、性别等因素来预测理想的体重,然后根据实际的体重和理想的体重之间的差距来制定合理的饮食和运动计划。
线性回归有哪些优缺点?线性回归有以下优缺点:
优点:
1、简单易懂,模型形式直观,可以直接看出因变量和自变量之间的关系。
2、计算速度快,不需要复杂的迭代过程,可以直接求出参数的解析解。
3、可以用来分析自变量对因变量的影响程度和方向,有利于探索数据的内在规律。
缺点:
1、对数据的线性假设过于严格,如果数据不符合线性关系,那么模型的效果会很差。
2、对异常值和多重共线性敏感,如果数据中存在异常值或者自变量之间存在高度相关性,那么模型的稳定性和准确性会降低。
3、模型的表达能力有限,不能捕捉复杂的非线性关系,需要引入高次项或交互项来增加模型的复杂度。
总结线性回归是机器学习中的经典算法,它可以用来建立因变量和自变量之间的线性关系模型,从而进行预测或分析。线性回归有许多实际应用,例如房价预测、广告效果评估、股票预测等。线性回归也有自己的优缺点,优点是简单易懂、计算速度快、可以分析变量的影响程度和方向;缺点是对数据的线性假设过于严格、对异常值和多重共线性敏感、模型的表达能力有限。因此,在使用线性回归时,我们需要注意检验数据是否符合线性回归的条件,以及选择合适的自变量和参数。希望这篇文章能够帮助你更好地理解和使用线性回归算法。
如果你喜欢这篇文章,希望可以关注一下,如果你想了解其他内容,也欢迎留言。
,