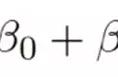编辑导语:在日常工作中,很多时候都会用到数据分析的方法,线性回归模型看起来非常简单,但实际上它的十分重要;本文作者分享了关于如何用线性回归模型做数据分析的方法,我们一起来学习一下。

线性回归是利用线性的方法,模拟因变量与一个或多个自变量之间的关系;对于模型而言,自变量是输入值,因变量是模型基于自变量的输出值,适用于x和y满足线性关系的数据类型的应用场景。
线性回归应用于数据分析的场景主要有两种:
- 驱动力分析:某个因变量指标受多个因素所影响,分析不同因素对因变量驱动力的强弱(驱动力指相关性,不是因果性);
- 预测:自变量与因变量呈线性关系的预测;
模型数学形式:????=????0 ????1????1 ????2????2 ⋯ ????????????????
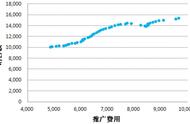
例如要衡量不同的用户特征对满意分数的影响程度,转换成线性模型的结果可能就是:分数=-2.1 0.56*年龄。
线性回归模型分为一元线性回归与多元线性回归:区别在于自变量的个数。

我们知道了模型的公式,那么模型的系数是如何得来呢?我们用最小二乘法来确定模型的系数——最小二乘法,它通过最小化误差的平方和寻找数据的最佳函数匹配,利用最小二乘法可以求得一条直线,并且使得拟合数据与实际数据之间误差的平方和为最小。
将上述模型公式简化成一个四个点的线性回归模型来具体看:分数=-2.1 0.56*年龄

最小二乘法选取能使模型 误差平方和= ????1???? ????2???? ????3???? ????4????最小化的直线,生成直线后即可得出模型自变量的系数和截距。
三、决定系数R方(R-squared)与调整R方R方(适用一元线性回归)。
R方也叫决定系数,它的主要作用是衡量数据中的因变量有多准确可以被某一模型所计算解释。
公式:
离差平方和:代表因变量的波动,即因变量实际值与其平均值之间的差值平方和。
误差平方和:代表因变量实际值与模型拟合值之间的误差大小。
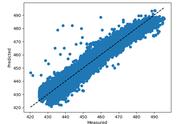
故R方可以解释因变量波动中,被模型拟合的百分比,即R方可以衡量模型拟合数据的好坏程度;R方的取值范围<=1,R方越大,模型对数据的拟合程度越好。
使用不同模型拟合自变量与因变量之间关系的R方举例:
R方=1 模型完美的拟合数据(100%)