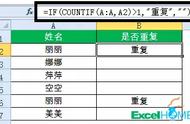
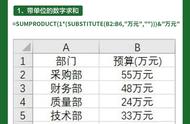
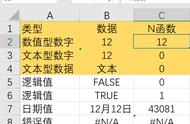
本人之前,没有人能对调和级数Σ1/n进行全覆盖式分级,更没有人能给出1/n的子级数以任何求和公式;本人以简单而充分的逻辑给Σ1/n进行了多种多样的分级(包括中华级数ABC型及其它方式)、并给出了各自对应的求和公式,所以,一切关于调和级数Σ1/n的无穷分级方法、及其对应求和公式的知识产权都属于中华数学!Σ1/n是欧系最重要的基础课题,欧洲人没能解决的问题中国人给他们解决了,用一个学术用语这叫“去敌对阵营插旗”。

本人已经把中华数学旗帜插上欧系阵地
Σ1/n有无限多种分配率结合率,可以二二、三三、四四,也可以一二三四、一三五七、二四六八,或者其它任意组合,只要有通项都是它的子级数,这包括中华级数A、B、C型,但是欧洲人创造的“调和放缩法”不在此列,因为它没有通项。
无论对Σ1/n进行怎样的分配率结合法,所形成的子集级数都绝对收敛,而且所有的子级数都有属于自己的求和公式。以下说的是最随意的“任意倍率分级”与它的求和公式。

本人关于任意1/n级数“倍率分级”文章
“a倍率”,就是以任意1/n为起点、以a为倍率的子集,如a=5、n=6,该子集为1/6.1/30.1/150.….1/6*5^k。该子集的求和1/6 1/30 1/150 … 1/6*5^k=5/6(5-1)=5/24。本方法适用于一切1/n级数的任意倍率分级,故可归纳总结该方法的求和公式为:Σ1/n*a^k=a/n(a-1),写作Σ(1/n.a)=a/n(a-1),它的内涵是:子级数的首项值为该级数值的(a-1)/a倍。

任意倍率级数求和公式概述
任意倍率分级而来的子集级数绝对收敛,Σ1/n子级数总值与总级数Σ1/n严格相等无丝毫差失,此例可证明调和级数极限值毫厘不爽、绝对收敛,欧系数学在这里采用的玩猫腻、和稀泥、打马虎眼等手段实属无赖无耻、凸显智商缺陷。
,