功的计算公式W= Flcosα只能用于恒力做功情况,对于变力做功,不能用W=Flcosα来计算功的大小.
一、将变力做功转化为恒力功
求某个过程中的变力做功,可以通过等效法把求该变力做功转换成求与该变力做功相同的恒力的功,此时可用W= Flcosα求功.等效转换的关键是分析清楚该变力做的功到底与哪个恒力的功是相同的
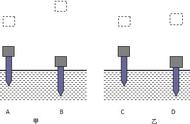
例:人在A点拉着绳通过一定滑轮吊起质量m=50kg的物体,如图所示,

开始绳与水平方向夹角为60°,当人匀速提起重物由A点沿水平方向运动s=2m而到达B点,此时绳与水平方向成30°角,求人对绳的拉力做了多少功?
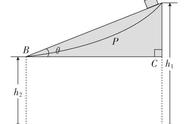
解析:人对绳的拉力大小虽然始终等于物体的重力,但方向却时刻在变,而已知位移x方向一直是水平的,所以无法利用W= Flcosα直接求拉力的功.若转换一下研究对象则不难发现,人对绳的拉力的功与绳对物体的拉力的功是相同的,而绳对物体的拉力是恒力.设滑轮距地面的高度为h,则h(cot30°-cot60°)=s
人由A走到B的过程中,重物上升的高度△h等于滑轮右侧绳子增加的长度,即:
△h=h/sin30°-h/sin60°
人对绳子做的功为:
=mg·△h=1000(√3-1)J≈732J
二、平均力法
当力的方向不变,大小随位移按线性规律变化时,可先求出力对位移的平均值F=
(F₁+F₂)/2,再由W=Flcosα计算功,如弹簧弹力做的功.
需要注意的是,若该力的大小随时间按线性规律变化,则不能通过求变力F对时间平均值来计算功.
例:用铁锤将一铁钉击入木块,设木块对铁钉的阻力与铁钉进入木块内的深度成正比。在铁锤击第一次时,能把铁钉击入木块内1cm。问击第二次时,能击入多少深度?(设铁锤每次做功相等)
【解析】考查对变力做功的计算及理论联系实际抽象建立模型的能力。
方法:平均力法


三、图像法
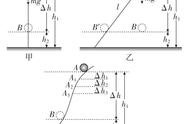
在v-t图象中图线与t轴所围图形的面积表示位移,由此我们得出,在F-l图象中图线与l轴所围图形的面积表示力F所做的功,如图甲所示,在轴上方的面积表示力对物体做正功,在轴下方的面积表示力对物体做负功.如果F-l图象是一条曲线,表示力的大小随位移不断变化,在曲线下方作阶梯形折线,折线下方每个小矩形面积分别表示相应恒力做的功.如图乙所示,当梯形折线分得越来越密时,这些矩形的总面积越趋近于曲线下方总面积,可见,曲线与坐标轴所围面积在数值上等于变力所做的功在图丙中轴上方的面积表示力对物体做正功的多少,l轴下方的面积表示力对物体做负功的多少,力对物体做的总功是l轴上方面积与l轴下方面积之差.