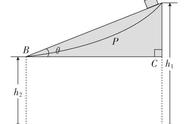
图甲可得重力和位移方向一致,可以用W=Fl来计算功,可以得出WG=mgΔh=mgh1-mgh2。
图乙物体沿斜面运动的距离是l,在这一过程中重力做的功是WG=(mg cos θ)l=mgΔh=mgh1-mgh2,从B′沿水平方向运动到B的过程中,重力不做功,所以整个过程重力的总功仍然是WG=mgh1-mgh2。
把图丙无限细分为若干个小斜面(图乙的情景),沿每个斜面运动时重力的功加起来就是从A运动到B重力做的功。
WG=mgΔh1+mgΔh2+mgΔh3+…
=mg(Δh1+Δh2+Δh3+…)
=mgΔh
=mgh1-mgh2。
得出结论:
1.物体运动时,重力对它做的功只与物体运动的始末位置有关,而与物体运动的路径无关。
2.重力做功与路径无关的理解:通常情况下,重力是恒力,而恒力做功W=Fl cos α,就是力F与在力F方向上的位移的乘积,而重力方向上的位移与路径无关,只与高度差Δh有关。
3.重力做功的特点可以推广到任一恒力做功,即恒力做功的特点为:与物体运动的具体路径无关,只与起点和终点两个位置有关,恒力做的功等于力与沿着力方向的位移的乘积。
4.物体在同一水平面上运动时,重力总是不做功。
5.物体的竖直位移等于零,则重力做功的代数和等于零,但过程中重力并不一定不做功。
值得注意的是:在物体运动的过程中重力可能会反复做正功、负功,但是这些正功、负功高度差相同的部分就会抵消,无论往复多少,最后只看始末位置的高度差;往上运动重力做负功,往下运动重力做正功,其值都为mgΔh,Δh为始末位置的高度差。