【规律方法】
1.解题的关键在于熟练地找出图形中的相等向量,并能熟练运用相反向量将加减法相互转化.
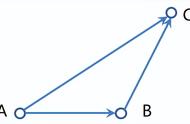
2.用几个基本向量表示某个向量问题的基本技巧:(1)观察各向量的位置;(2)寻找相应的三角形或多边形;(3)运用法则找关系;(4)化简结果.

考点三 共线向量定理及其应用
【规律方法】
1.证明三点共线问题,可用向量共线解决,但应注意向量共线与三点共线的区别与联系,当两向量共线且有公共点时,才能得出三点共线.
2.向量a,b共线是指存在不全为零的实数λ1,λ2,使λ1a+λ2b=0成立.

【反思与感悟】
1.向量线性运算的三要素
向量的线性运算满足三角形法则和平行四边形法则,向量加法的三角形法则要素是“首尾相接,指向终点”;向量减法的三角形法则要素是“起点重合,指向被减向量”;平行四边形法则要素是“起点重合”.
2.三个常用结论
(1)O为△ABC的重心的充要条件是++=0;
(2)四边形ABCD中,E为AD的中点,F为BC的中点,则+=2;
(3)对于平面上的任一点O,,不共线,满足=x+y(x,y∈R),则P,A,B共线⇔x+y=1.
注意向量共线与三点共线的区别.
【易错防范】
1.解决向量的概念问题要注意两点:一是不仅要考虑向量的大小,更重要的是要考虑向量的方向;二是考虑零向量是否也满足条件.要特别注意零向量的特殊性.
2.在利用向量减法时,易弄错两向量的顺序,从而求得所求向量的相反向量,导致错误.