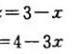2
汽车从静止开始加速,然后慢慢停下来,速度与时间存在函数关系,如有v(t)=t(14-t),图像如下:

以上的图像,f(t)=t(14-t)的图形是一条曲线,我们称之为非线性关系或曲线关系。
所以我们来考虑t(14-t)与t的变化率(导数)。与线性关系的变化率是常量不同,非线性关系的变化率变得复杂。我们使用

来求解,可求得t(14-t)与t的变化率是:14-2t。当t取不同值时,反映f(t)在该值附近相应的变化量是14-2t。当t=7时,该值附近的变化率为0。t在7的前段是正相关关系,后半段是负相关关系。

导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话,函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率 。导数的本质是通过极限的概念对函数进行局部的线性逼近。例如在运动学中,物体的位移对于时间的导数就是物体的瞬时速度。
通过导数可以判断函数的单调性、凹凸性、最大值、最小值。
曲线下的面积,就是汽车从静止到加速,再到减速,再停下来后经过的距离。
我们做一个大概的估算,时间是14秒,平均速度估计33m/s,则距离大概是462m.
如果按微积分的思路:
由(t(14-t))'=14-2t=0,求得当t=7m时,汽车的最大速度是49m/s。速度v∈[0,49],时间[0,14]。
我们要求一个表达式F(t),其导数F'(t)刚好等于f(t),也就是t(14-t):