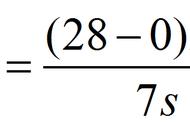当 x = -3/2 时,d 取最大值,△APB 面积最大,此时 P 点坐标为 (-3/2 , 7/4).
注:
在解决实际问题时要注意确定自变量取值范围的方法,本题是由直线与抛物线的交点来确定的,这样才能确定定义域内的最值 .
三、利用二次方程的判别式
欲求函数 y = f(x) ( x ∈ R ) 的极值,如果可以把函数式整理成关于 x 的二次方程,
注意到 x 在其定义域内取值,即方程有实根,
所以可以通过二次方程的判别式 △ ≥ 0 来探求 y 的极大值与极小值 .
【例题4】已知 0 ≤ x ≤ 1 , 求

的最值 .
解:原式可化为

∵ x ∈ R ,
∴

解得 y ≤ 1/4 或 y ≥ 9/16 ,
即函数 y 的值域为 y ≤ 1/4 或 y ≥ 9/16 ,
∴ y极大 = 1/4,y极小 = 9/16 .
当 y = 1/4 时,代入原函数解析式得 x = 1 ∈ [ 0 , 1 ] ;
当 y = 9/16 时,代入原函数解析式得 x = -1 ∉ [ 0 , 1 ] .
又 x = 0 时 , y = 2/3 ,
∴ 当 x = 0 时,y 取极大值 2/3 .
注:
① 由判别式确定的是函数的值域,由值域得到的是函数的极值而不是最值;
② 对有些函数来说,极值与最值相同,而有的函数就不一定,
如本题中的极大值比极小值还小,这是因为极值是就某局部而言;
③ 若要求函数在给定的定义域内的最值,一定要注意极值是否在此定义域内取得,
即要注意验根 .
四、利用重要不等式
【例题5】设 x , y , z ∈ R , 且 2x 4y 9z = 16 .
求 6√x 4√y 3√z 的最大值 .
解:
令 u = 6√x 4√y 3√z ,