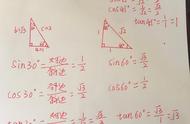我国著名数学家华罗庚先生说过"数缺形时少直观,形缺数时难入微",这也就是我们常说的数形结合思想.数形结合思想运用非常广泛,这里所说的用"数"解"形"只是其中一个具体应用,在这里我们不仅可以理解为借助方程和函数知识解答几何问题,还包括借助代数式的恒等变形解答几何问题.学会这种方法,养成用"数"解"形"的习惯,不仅可以在中考中获益,而且对以后的学习也会帮助很大.

类型1 借助方程,用"数"解"形"
例1. 如图,O为△ABC内一点,OA=OB=OC,BO⊥CO,OD⊥AB于点D,DO交AC于点E,已知BC=3,AC=4,则AE的长为 _______

【解析】连接BE,易得EB=AE,∠EAO=∠ECO=∠EBO,
∵∠ECB ∠EBC=∠ECO 45° ∠EBC=∠OBE 45° ∠EBC=90°,∴∠BEC=90°,在Rt△BEC中,BC²-CE²=BE²,∴BC²-CE²=AE²,设AE=x,则3²-( 4-x ) ²=x²,
解得x=2 √2/2 或2-√2/2(不合题意,舍去)
【名师点拨】 当问题中涉及线段较多,要想表达清楚这些线段之间的数量关系,可设其中一条或多条线段为未知数,再由线段成比例得到等量关系,从而列出方程( 组 ),解出未知数,完成解题.

例2.(2018秋•嘉兴期末)如图,在一张直角三角形纸片ABC中,∠ACB=90°,BC=1,AC=√3 ,P是边AB上的一动点,将△ACP沿着CP折叠至△A1CP,当△A1CP与△ABC的重叠部分为等腰三角形时,则∠ACP的度数为 40°或70° .