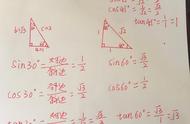【分析】分两种情形画出图形分别求解即可.
【解答】如图1中,当PC=CE时,设∠ACP=x.

∵CP=CE,∴∠CPE=∠CEP,
∵∠CPE=∠ACP ∠A=x 30,∴x x 30 x 30=180°,∴x=40°.
如图2中,当CP=CE时,设∠ACP=x.
则∠CPE=∠CEP=2x﹣90° 30°=2x﹣60°,
在△CPE中,90°﹣x 2(2x﹣60°)=180°,解得x=70°,
综上所述,∠ACP的度数为40°或70°,
故答案为40°或70°.
【点评】本题考查翻折变换,等腰三角形的判定和性质等知识,解题的关键是理解题意,学会用分类讨论的思想思考问题,属于中考常考题型.

牛刀小试:1.(2018秋•青羊区校级月考)如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=3,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F,若△AB′F为直角三角形,则AE的长为 .

【答案】9/2或21/5.
【提示】分两种情形分别画出图形求解即可、
如图1中,当∠AFB′=90°时.
如图2中,当∠AB′F=90°时,作EH⊥AB′交AB′的延长线于H.