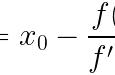这里的根 β 是单根,即 f( β ) = 0 且 f ' (β) ≠ 0,于是:

由于 γ (x) 的连续性可知,存在一个领域( β - δ,β δ ),对该领域内的任意 x ,都有 | γ' (x) < q |,其中 0<q<1,因此 γ (x) 为区间( β - δ,β δ ) 上的一个压缩映像,于是我们可以得到如下结论:

由此可见,牛顿迭代法的局部收敛性较强,所以只有初值充分地接近,才能确保所迭代序列的收敛性。为了放宽对局部收敛性的限制,必须再增加能够使该序列收敛的充分条件,

上式可以化为以下几种情况: