1、基本图形中的面积关系:

2、平行四边形背景下与面积相关的问题:
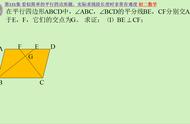
① 如图,在平行四边形ABCD中,点F在DC延长线上,联结AF交BC于点E,联结BF,DE,求证:S▲ADE=S▲BAF.
解析:要证明▲ADE的面积=▲BAF的面积,从图中可以看出这两个三角形的面积都等于平行四边形面积的一半,所以结论可证。

② 如图1,E为平行四边形ABCD内一点,试探索▲ADE、▲BCE、▲ABE、▲DCE面积之间的关系;如图2,E在平行四边形ABCD边CD所在直线上方,试探索▲ADE、▲BCE、▲ABE、▲DCE面积之间的关系.

解析:借由前面的解题思路,通过过点E作垂线,计算四个三角形的面积,用平行四边形的边长表示相应的面积。