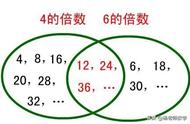
五年级上册︱教材为什么把倍数和因数的研究界定在非零自然数的范围内呢?
实际上,与其说是给倍数和因数界定适用范围,不如说倍数和因数是研究这个范围内的数之间关系的产物。
一个整数的倍数的个数是无穷多的,其中最小的倍数是这个整数的本身。
首先我们要明确的是,五年级我们所学习的“倍数”,和二年级我们所学习过的“倍”,是两个不同的概念。
例如,4 的倍数有 4,8,12,16,…如何描述这些 4 的倍数之间的区别呢?这就需要引入“倍”的概念,4 是 4 的 1 倍的倍数,8 是 4 的 2 倍的倍数,12 是 4 的 3 倍的倍数等。可见,“倍数”与“倍”是不同的两个概念。
12÷4=3,其中 12 是 4 的倍数,12 也是 4 的 3 倍。“3 倍”是刻画 12 和 4 之间的数量关系的,可以画图表示 12 是 4 的 3 倍(如图1)。

图 1

六年级上册︱如何带领学生经历圆的周长的探索过程?
从数学的历史发展和学生的认识发展上来说,圆的周长是难点。虽然人们很早就发现轮子越大滚一圈越远,但是一直没有找到计算周长的方法。为此数学家一直在探索,最终发现圆的周长与直径之间的关系。教材设计圆的周长这一内容,正是对这一过程的浓缩,引导学生充分经历圆周长的探索过程,帮助学生积累数学活动经验。
活动经验总是伴随着活动而产生,只有数学活动才会产生数学活动经验。积累数学基本活动经验,要求人们能“从头到尾”的思考问题:开始的条件是什么,目标的结果是什么,过程如何设计,等等1。为此,教材设计了很多活动,意在拉长结论获得的过程,帮助学生积累相关的数学活动经验。圆的周长这一内容正是出于这样的考虑才安排 2 课时教学,第 1课时只是探索出圆的周长与直径的关系,而周长的公式与利用公式进行计算安排在第 2 课时,拉长了探索圆的周长与直径关系的探索过程,让学生有充足的时间体会人类重要的数学知识发生、发展的脉络。

“圆的周长”第 1 课时