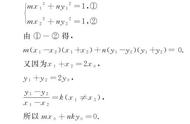全文共1265字,预计阅读时间:4分钟
之前我们学习了什么是立体图形和七个简单几何体,还学习了立体几何图形的直观图及其表面积和体积的计算,为了保证学习效果,同学们要及时回顾,同学们还有哪些疑问也可以留言提出哦!
今天,我们重点来研究一下什么是面以及点、直线和平面在空间上的位置关系吧!

在日常生活中我们常常能接触到平面,在数学中我们常用平行四边形来表示平面,其中在表示水平放置的平面时,我们常将其一边画为横向的,在表示竖直放置的平面时,我们常将其一边画为竖向的。
一般的,我们会使用小写的希腊字母α、β、γ等来表示平面,也可以用大写英文字母表示平行四边形的顶点,并使用四个顶点或者相对的两个顶点的大写英文字母表示平面。
在日常生活中,我们可以发现关于平面的以下三个基本事实:
1)过不在一条直线上的三个点,有且只有一个平面;
2)如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内;
3)如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
由这三个基本事实,我们可以得到三个推论:
1)经过一条直线和这条直线外一点,有且只有一个平面;
2)经过两条相交直线,有且只有一个平面;
3)经过两条平行直线,有且只有一个平面。
其实,上面的三个推论都是“三个不共线的点能确定一个平面”的扩展。

我们之前学习过点和直线的位置关系,分别是点在直线上和点在直线外,简单的,点和平面的位置关系也有这两种。
显然,在空间中直线和直线的位置关系就更加复杂了。
曾经我们在同一平面内研究过两直线的位置关系,分别为相交和平行,而将两直线放在空间中的不同平面时,无论它们有没有公共点,它们都不是平行的,我们称之为异面直线。
因此,在空间中,两直线的位置关系有以下三种:
1)相交直线:在同一平面内,有且只有一个公共点;
2)平行直线:在同一平面内,没有公共点;
相交直线和平行直线都是共面直线;
3)异面直线:不同在任何一个平面内,没有公共点。

类似点与直线的位置关系,直线与平面的空间位置关系也分为两大类,分别是直线在平面内和直线在平面外。
当直线在平面内,我们可以发现直线和平面有无数个公共点;
当直线在平面外时,我们可以发现直线可以与平面只有一个公共点,也可以与平面没有公共点;
那么当直线与平面有且只有一个公共点时,我们称直线与平面相交;
当直线与平面没有公共点时,我们称直线与平面平行。

空间中平面与平面的位置关系类似于在同一平面中直线与直线的位置关系,分别为平行和相交。
当两个平面没有公共点时,我们称两个平面平行;
当两个平面有一条公共直线时,我们称两个平面相交。

今天,我们学习了平面的定义以及点、直线、平面在空间中的位置关系,希望今天的内容可以帮助同学们更好的进行高中数学学习哦!
同学们有任何不懂的内容可以留言提问,如果有需要的话我们会有习题类推文哦!
下一期我们将继续讨论数学学习的相关问题呀!如果你想知道更多,请关注我们哦!
本文由如意王工作室原创,欢迎关注,带你一起长知识!