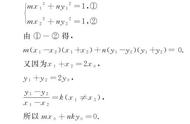角度2 由异面直线所成角求其他量

【规律方法】 用平移法求异面直线所成角的一般步骤:
(1)作角——用平移法找(或作)出符合题意的角;
(2)求角——转化为求一个三角形的内角,通过解三角形,求出角的大小.


【反思与感悟】
1.主要题型的解题方法
(1)要证明“线共面”或“点共面”可先由部分直线或点确定一个平面,再证其余直线或点也在这个平面内(即“纳入法”).
(2)要证明“点共线”可将线看作两个平面的交线,只要证明这些点都是这两个平面的公共点,根据公理3可知这些点在交线上.
2.判定空间两条直线是异面直线的方法
(1)判定定理:平面外一点A与平面内一点B的连线和平面内不经过点B的直线是异面直线.
(2)反证法:证明两线不可能平行、相交或证明两线不可能共面,从而可得两线异面.
3.求两条异面直线所成角的大小,一般方法是通过平行移动直线,把异面问题转化为相交直线的夹角,体现了化归思想.
【易错防范】
1.异面直线易误解为“分别在两个不同平面内的两条直线为异面直线”,实质上两异面直线不能确定任何一个平面,因此异面直线既不平行,也不相交.
2.直线与平面的位置关系在判断时最易忽视“线在面内”