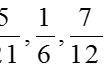图4
想一想:
问题1⃣️:所有的分数都能化成有限小数吗?
问题2⃣️:能转化成有限小数的分数的分子、分母具备哪些特征呢?
基于我们前面探讨的有限小数如何化分数(见图3)的内容,现在理解哪些分数可以化成有限小数也不是什么难题。我们可以先来挑战一下几道题(见图5)来感受一下,哪些分数可以化成有限小数,这样的分数有什么特征?

图5
不难发现,能化成有限小数的分母,都是可以转化成10、100、1000……10^n的。而将10^n分解质因数后,不难发现,它质因数组成只有2和5。分母的特征我们已经找到了,那能化成有限小数的分数的分子有什么要求吗?分子有没有什么要求。
等等,接下来这个情况(见图6)好像不太符合我们刚才总结的规律:

图6
仔细观察后不难发现,12/15这个分数并不是最简分数,经过化简,12/15可以转化成4/5,是可以化成有限小数的,所以,刚刚的规律有个非常重要的前提条件:我们探讨的是哪些最简分数可以化成有限小数。
综上,最简分数a/b,若分母a中不含2和5以外的质因数,则这个分数可化成有限小数;若分母a中含除2、5以外的质因数,则这个分数不可以化成有限小数。
上面这个结论是否严谨,作为数学老师,还是需要验证一下(验证过程见图7),学生不做要求。

图7
2.经过多少次都除不尽的分数——可以化成无限循环小数。
无限循环小数分为纯循环小数和混循环小数。
1⃣️我们先来讨论纯循环小数与分数的关系: