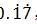1,无限循环小数为什么会出现?
我们知道,所有的有理数都能写成分数,但有些分数是有限小数,比如1/5=0.2;有些分数是无限循环小数,比如1/3=0.333…。不管有限还是无限,这些数都不过是数轴上的一个点,无限小数并没有什么必然特殊的地方。之所以有些分数写成小数就是比另一些分数难表达,之所以无限循环小数会出现,是因为符号的表达问题,是由于进制导致的。比如2/9=0.222...,但如果使用九进制,那么2/9就等于0.2,没有循环了。在十进制下的任何一个无限循环小数,都可以转化为另一种进制下的有限小数。
因为10只能被2和5整除,所以3、7、13这些不能被十进制整除的数,就会除不尽而成为无限循环小数。如果用9进制,那么3、9、27为分母的数,就可以被除尽了,2、5为分母的数反而成为无限循环小数。用21进制,那么以3和7的任意倍数为分母的数也变成有限小数了。
或者可以这样理解,在十进制下,把一个分数化成小数,也就是把分母化为一个10的n次方数(n是不小于1的整数),分子就是小数部分。比如把1/2化成小数,由于1/2=5/10,于是等于0.5;把1/8化成小数,由于1/8=125/1000,于是等于0.125。这样就很好理解了,为什么1/3是无限循环小数,因为3的倍数里,没有一个数正好等于10的任意正整数次方。同理,作为分母的数,如果含有3、7、11为因数,那么它就会变成无限循环小数。事实上,由于10只能被2和5除尽,所以任何含有2和5以外的素因数的分母,都会导致出现无限循环小数,比如5/6,10/11,3/26。由这种方法我们可以判断,任意一种进制下,哪些分数是有限小数,哪些是无限循环小数。也可以判断某个无限循环小数,要哪种进制才可以转化为有限小数。
当然,前提是已经把分数化为最简,例如13/26就不是循环小数,13/26实际上是1/2。
数学是一种工具,使用几进制是一种约定。我们选择了十进制,并不代表十进制在数学上最完备,可能只是因为人有十个指头。使用哪种进制会影响人的思考方式,如果一种使用12进制的外星人,就会觉得以数量12为一组比10“自然”得多,他们处理3的速度,就远高过处理5的速度。
如果使用30进制,就可以同时被2、3、5整除。也许有某个智商很高的外星人,经常要处理较大的数,他们使用了2310进制(2*3*5*7*11=2310)。好处是处理2、3、5、7、11或它们之间任意几个数的公倍数,都不会遭遇无限小数了。然而,2310进制不仅个位数就要记得2310个符号,而且给背下2309*2309乘法表!这可实在太难了,和我们的9*9乘法表相比。转发
,