作者 | [美]威廉·邓纳姆(Willian Dunham)
翻译 | 冯速
来源 | 节选自《数学那些事:伟大的问题与非凡的人》,人民邮电出版社,2022年3月。[好玩的数学]获授权转载,在此感谢!

首先, 伯努利试验不是佛罗伦萨的一道法律程序, 而是初等概率论的基础, 在我们对不确定世界的理解中起着重要的作用。
伯努利试验是一个有两种结果的简单试验。它的结果是成功或失败, 黑或白, 开或关。没有中间的立场, 没有妥协的余地, 没有优柔寡断的安慰。
这样的例子太多了。我们观察从一副纸牌中拿出的一张牌, 它或是黑色或是红色。我们接生一个婴儿, 这个婴儿或是女孩子或是男孩子。我们经历24小时的一天, 或者遇到流星或者遇不到流星。在每一种情况下, 很方便设计一种结果为“成功”, 另外一种结果为“失败”。例如, 选出一张黑色牌、生一个女儿、没有遇到流星都可以标识为成功。然而, 从概率的角度看, 选择红牌、儿子或者遇到流星为成功也是不会产生差异的。在这种场合下, 成功一词没有价值取向的色彩。
单个伯努利试验没有太大的意义。然而, 当我们反复进行伯努利试验, 并观察这些试验有多少是成功的、多少是失败的, 事情就变得很有意义了, 这些累计记录包含很多潜在的非常有用的信息。
当我们做试验时, 有一个关键的条件:这些重复的试验必须是相互独立的。独立一词不仅有专业定义, 而且还传达了适合我们目标的含义:如果一个事件的结果绝不会对另一个事件的结果产生影响, 那么这两个事件就是相互独立的。例如, 史密斯生一个儿子与约翰逊生一个女儿是两个相互独立的事件。又例如, 投掷一枚一角硬币与投掷一枚一分硬币的结果(正面或反面)也是相互独立的, 一枚硬币的结果不会对另一枚硬币的结果产生影响。
但是, 如果我们研究一副纸牌中的两张牌, 一次只能抽一张, 并认为黑色纸牌是成功, 那么在抽完第一张纸牌后再抽第二张纸牌时, 独立性就丧失了。这是因为, 如果第一张牌是梅花A(一次成功), 那么它将影响第二次的抽取结果——它使得第二次抽出黑色纸牌的可能性减小, 第二次抽出A的可能性也减小, 而且绝对不可能还是抽到一张梅花A。
幸运的是, 这种独立性的缺失可以通过一个简单的对策加以弥补。在抽取第一张纸牌之后, 把它放回到原来的纸牌中, 重新洗好, 然后再抽。因为我们的第一张纸牌已经重新混入到原来的纸牌中, 所以它的身份对第二次抽取已经不再产生影响。在这种意义下, 独立事件要求为每一次试验创造一个不留痕迹的平台, 从而使得每次试验成功的概率保持相同。
伯努利试验最鲜明的例子出现在博弈游戏中, 例如投掷硬币或者骰子。对于硬币来说, 每一次投掷显然是独立的, 因此在每次投掷时成功的概率(比如说得到正面的概率)是相同的。说一枚硬币是“平衡的”, 意思是这个概率正好是1/2。对于一枚均匀的骰子, 如果我们指定投出3是成功, 那么我们成功的概率总是1/6。
但是, 如果我们投掷一枚硬币五次会发生什么呢?在这五次投掷中得到三个正面和两个反面的概率是多少呢?推而广之, 如果我们投掷这枚硬币500次, 得到247次正面和253次反面的概率是多少呢?这是一个看似噩梦般的问题, 但是它的解却出现在早期的概率论杰作之一——雅各布 • 伯努利(Jakob Bernoulli, 1654—1705)的《猜度术》之中。
伯努利是瑞士本土人, 他的祖父、父亲和岳父都是富裕的药剂师。他抛弃了臼和研棒, 去大学研究神学, 并于22岁那年获得了学位。然而, 尽管他的家族都与医药有关, 并且他接受的是布道方面的教育, 但他真正感兴趣的却是数学。
从17世纪70年代末开始直到去世, 伯努利一直都是世界上最杰出的数学家之一。他是一个天才, 却有着令人讨厌的个性, 他目空一切, 对那些不具天赋的人的努力嗤之以鼻。例如, 在研究了我们今天所谓的“伯努利数”(为了纪念他而命名)之后, 伯努利找到了对正整数幂求和的一种非常巧妙的捷径。他说“自己用了不到七分半钟”就确定了前1000个正整数的十次幂的和。也就是说, 他用了不到十分钟就确定了下面的结果:
这的确是个巨大的和。但是他在一份亲自主笔的评论中自我标榜说他的捷径“清楚地表明布里奥的工作是多么无用……他(布里奥)不过是费了好大劲计算了上面的前六个幂的和, 而我用一页纸就完成了全部计算”。这个人对可怜的伊斯梅尔 • 布里奥(Ismael Bullialdus)没有一点同情心, 他不仅拥有一名数学家的非凡洞察力, 而且也不同寻常地自负。
雅各布 • 伯努利的巅峰时期正是戈特弗里德 • 威廉 • 莱布尼茨发现微积分的时期, 雅各布是普及这一丰硕成果的重要人物之一。同任何新发展起来的理论一样, 微积分得益于那些紧跟其首创者脚步的人, 得益于那些才华不如莱布尼茨的学者, 他们的贡献是对这一门学科加以整理, 这是必不可少的。雅各布就是这样一位贡献者。

[瑞士, 巴塞尔, Birkhäuser Verlag AG出版社许可翻印, 这是1969年由弗莱肯施泰因(J.O. Fleckenstein)编辑的《雅各布 • 伯 努利全集, 卷1:新星, 自然哲学》中的一幅画像]
在这项事业中, 他有一位令人不安的同盟者约翰(Johann, 1667—1748)——他的弟弟, 与他的名字首字母相同, 这就是极富才华但爱争吵的伯努利兄弟。事实上, 雅各布曾充当他弟弟的数学老师的角色。在之后的岁月里, 他也许后悔把约翰教得如此好, 因为事实证明这位弟弟是一位与他不相上下的数学家, 甚至也许超过了他。兄弟二人为争夺数学霸权展开了激烈竞争。当约翰解决了曾经难倒哥哥的某个问题时, 他总是毫不掩饰自己的兴奋, 尽管雅各布故意叫约翰为他的“小学生”, 暗示约翰只是在效仿他这位导师。这两个伯努利都算不上是高尚的人。
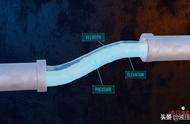
一次著名的冲突起源于悬链线的问题。悬链线是固定在墙上两点的悬链所形成的曲线(见图B-1)。熟悉代数的人也许猜测这条链沿着一条抛物线弧垂悬, 这样一个完美的合乎逻辑的猜测早在17世纪初就被伽利略这样的人物想到了。但是这样悬挂的链其实不是抛物线, 到了1690年, 雅各布 • 伯努利正在为确定这条曲线的真实身份而非常努力地研究着, 也就是说, 他要给出它的方程。

图 B-1
事实证明, 雅各布不能胜任这项任务。当约翰给出答案时, 不难想象雅各布惊讶的样子。后来约翰在炫耀他的胜利时说, 为了这个解决方案“我全身心地去研究, 整晚不休息”。他气人的本领与他的才华一样出色, 约翰匆匆忙忙跑到雅各布面前, 告诉一直苦思冥想的哥哥问题的答案。雅各布一下子垂头丧气。
但是, 雅各布要实施他的“报复”。这一次的战场是所谓的等周问题, 说的是从有相同周长的曲线中, 区分出哪条曲线围出的面积最大。我们将在第I章中更详细地讨论这个问题, 但是现在可以先看一下雅各布 • 伯努利在1697年是如何运用微积分来描述这个问题的。他要对付一个难缠的叫作三阶微分方程的数学对象, 这项工作为一个现在称为变分法的新数学分支指出了道路, 这一分支有着广泛的研究前景。
弟弟约翰与他的意见不同, 并说已经用一个相对简单的二阶微分方程解决了这个等周问题。如同以往伯努利家的情况一样, 他们的争吵变成对抗, 最终只是因为缺少“弹药”而停止。