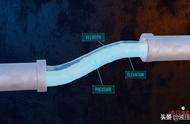
图B-2
我们将用概率方法估测它的面积。首先, 如图所示在的矩形内圈出一个区域。其次, 任由计算机在这个矩形内寻找任意多个(x,y)点。例如计算机也许能够找出如图所示的两个点A=(3.5,7.3), B=(6.0,13.7)。
现在, 我们要问计算机:这些随机的点是落在这个湖内还是落在了湖外?在我们的例子中, 这个问题很容易解决。检验点A, 我们在抛物线方程中令x=3.5,于是求得对应的值。这表明点(3.5, 15.75)在抛物线上。于是比对点A来说, 点A的第一个坐标相同, 而第二个坐标只有7.3, 它落在了抛物线的里面, 即在湖内。
类似地, 当考虑点B时, 我们在抛物线方程中代入它的第一个坐标, 得到对应值。因此点(6, 12)在抛物线上, 所以点B(6,13.7)落在抛物线外面, 砸到了干*地上。计算机只需要几毫秒的时间, 就能选择很多随机的点, 并确定它们是在湖内还是在湖外。
现在看一下根据蒙特卡罗方法的关键观测:随机选出的点落入湖内的精确概率记为p, 它是湖面占据矩形的面积的比例, 即

当然, 我们只有先知道这个湖的面积(这正是我们要求的未知量)才能计算出这个概率。但是, 我们能够根据x/N来估测点落入湖中的概率p, 即落入抛物线内部分的比例。利用长期的成功比例来近似真实概率, 这本身就是大数定律的直接运用。
对于这个例子, 我们的计算机在矩形内选出500个点, 而且发现其中有342个点落入湖内。因此, 我们估测

经过交叉相乘之后, 这个估测值是

因此, 在没有借助其他任何东西, 只是利用了伯努利大数定律的情况下, 我们就得到了湖的面积的粗略的近似值。
我们如何能够得到一个更精确的估测值呢?我们只简单地让计算机在这个矩形内选出5000个点而不是500个点。在这个例子中, 它发现其中有3293个点在这个湖内, 因此得到