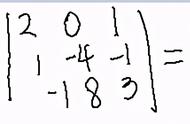我们在前三讲中主要讲了如下内容:
向量:就是一组量,水平排列就是行向量,竖直排列就是列向量。
我们规定了向量的内积或者数积:就是向量对位的乘积和。以此我们可以刻画向量的模,就是相同向量的内积再开根号。而向量的指向通过射影的概念,用两个向量的内积比两个向量的模来加以反映。两个向量的平行与正交也进行了定义。
矩阵:就是以列向量水平排列的行向量,反之也行。我们定义了幺阵,定义了矩阵的转置,矩阵的加减乘法,定义了矩阵的转置与矩阵的逆,这就建立了矩阵的基本运算规则。
对于向量,可以有平行关系,一般来说关系可以有相关与无关,相关的意思是:如果n个向量,其中一个向量可以用另外的向量线性组合表达出来,这n组向量就是相关的,反之是无关的。
N维空间就是指,给定n个相互独立的向量,其线性组合形成的所有向量构成一个n维向量集合,空间上可以定义向量的运算。这n个独立的向量叫做该空间的基底,空间是基底扩张形成的集合。
n维向量空间的基底如果相互正交,则表达线性空间的向量会比较方便,这涉及矩阵的正交化问题,我们后续会讲如何做。
注意到我们所涉及的内容大部分是从几何出发引申出来的,长度与方向已经有了很好的表达,但面积体积这样的概念却并没有包含在内。这涉及到向量的另外一种乘法:外积。本讲先回到线性代数的起点:解线性方程,我们讲行列式,行列式可以看成方形矩阵的自运算,用于实现矩阵值的量,国外多用determination这词来表达其与矩阵的关系。
二阶与三阶行列式定义:矩阵的行列式对应着一个方矩阵的值,设A是个n元矩阵,
就是这个矩阵的行列式值。下面我们将利用矩阵与行列式的概念重新看看一次方程的解。
二元一次方程组可以写成

并叫这个式子是二阶行列式的话,那么方程的解可以写成:

方程组有解的条件也变为