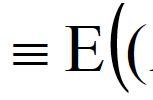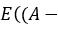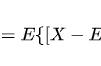上次写了相关系数,其实很类似的一个概念是协方差。要说协方差,先复习下基本的统计内容
1. 均值
2.方差(标准差、标准方差)
简单来说,标准差是一组数值自平均值分散开来的程度的一种测量观念。一个较大的标准差,代表大部分的数值和其平均值之间差异较大;一个较小的标准差,代表这些数值较接近平均值。
如果是样本,标准差公式根号内除以(n-1)。因为我们大量接触是样本,所以普遍使用根号内除以(n-1)。在统计学中样本的均差多是除以自油度(n-1),它的意思是样本能自由选择的程度。当选到只剩一个时,它不可能再有自油了,所以自油度是(n-1)。 【故意写错,通过不了没有办法啊】
3.协方差
可以看到方差是衡量单个变量的,或者说是自己和自己的分散程度。如果要分析多个变量之间的分散程度或者多个变量之间的关联程度,怎么办呢?类似方差,协方差就是
对比var(X),很容易发现它们的关系。 var(x,y) = COV(x,y),或者说方差是协方差的一个特例。
x = 3 2 4 5 6
y = 9 7 12 15 17
首先计算x、y的期望值:
ux=(3 2 4 5 6)/5=4
uy=(9 7 12 15 17)/5=12
利用公式把xi(3、2、4、5、6)、yi(9、7、12、15、17)及如上计算得到的期望依次带入公式,算得

Excel文档说计算公式是
方差VAR 的计算公式如下:

协方差COV的计算公式:

相关系数的上半身和协方差的长得好像,确实只看上半部分。相关系数就不说了吧,见我另外一篇文章。
4.协方差矩阵
就是比协方差多了个矩阵,没错。协方差矩阵计算的就是多个变量之间的协方差,两两之间互相计算,最后就得到了一个矩阵。
比如,有a,b,c三个变量,计算cov(a,a) cov(a,b) cov(a,c) ... ... 就得到3*3的对称(对称,你懂的)矩阵,其实很简单吧。
cov(a,a) cov(a,b) cov(a,c)
cov(b,a) cov(b,b) cov(b,c)
cov(c,a) cov(c,b) cov(c,c)
————————————————