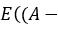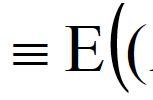今天是概率统计专题的第六篇,我们来看看方差相关的概念。
方差的定义方差在我们的日常生活当中非常常见,它主要是为了提供样本离群程度的描述。举个简单的例子,我们去买一包薯片,一般来说一袋薯片当中的数量是固定的。我们假设平均每袋当中都有50片薯片好了,即使是机器灌装,也不可能做到每一袋都刚好是50片,或多或少都会有些误差。而均值则无法衡量这种误差。
如果现在有两个薯片品牌,它们的口味都差不多,平均每袋也都是50片。但是其中A品牌的薯片有一半是80片,还有一半是20片。B品牌呢,99%都在45-55之间。你说你会买哪一个牌子呢?(在不考虑通过称重的情况下)。
在现代社会,凡是工厂出厂的产品,基本上都离不开方差这个概念。方差越低,说明工厂的生产能力越强,能够做到每一个产品都很精细,相反如果方差越大,则说明瑕疵很多,不够精细。也就是说,方差衡量的是样本距离均值的期望。
它本来应该写成:E|X - E(X)|。
但是由于式子当中存在绝对值,我们通常会对它平方,从而将绝对值消掉。写成:

这里的E表示期望,这是统计学当中的写法,如果看不明白,我们也可以把式子展开写成:

这里的N表示的是样本数量,X bar 是样本的均值。Var是英文variance的缩写,我们也可以写成D(X)。
由于方差是通过平方计算得到的,我们也可以将它进行开方,得到标准差。根号D(X),也可以写成σ(X)。
方差的性质关于方差有几个著名的性质,如果X是变量,而C是常数。那么:

也就是对于每一个变量都乘上一个常数,那么整体的方差扩大C的平方倍。这个很好理解,因为样本值扩大了C倍,由于我们在计算方差的时候用到了平方,那么自然就是扩大了C的平方倍。我们利用上面展开的公式代入可以很容易得到证明。
下一个性质是: