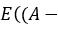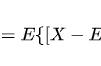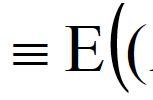本文介绍了几个重要的变量相关性的度量,包括皮尔逊相关系数、距离相关性和最大信息系数等,并用简单的代码和示例数据展示了这些度量的适用性对比。
从信号的角度来看,这个世界是一个嘈杂的地方。为了弄清楚所有的事情,我们必须有选择地把注意力集中到有用的信息上。
通过数百万年的自然选择过程,我们人类已经变得非常擅长过滤背景信号。我们学会将特定的信号与特定的事件联系起来。
例如,假设你正在繁忙的办公室中打乒乓球。为了回击对手的击球,你需要进行大量复杂的计算和判断,将多个相互竞争的感官信号考虑进去。为了预测球的运动,你的大脑必须重复采样球的位置并估计它未来的轨迹。更厉害的球员还会将对手击球时施加的旋转考虑进去。最后,为了击球,你需要考虑对手的位置、自己的位置、球的速度,以及你打算施加的旋转。
所有这些都涉及到了大量的潜意识微分学。一般来说,我们理所当然的认为,我们的神经系统可以自动做到这些(至少经过一些练习之后)。
同样令人印象深刻的是,人类大脑是如何区别对待它所接收到的无数竞争信号的重要性的。例如,球的位置被认为比你身后发生的对话或你面前打开的门更重要。
这听起来似乎不值得一提,但实际上这证明了可以多大程度上学习从噪声数据中做出准确预测。
当然,一个被给予连续的视听数据流的空白状态机将会面临一个困难的任务,即确定哪些信号能够最好地预测最佳行动方案。
幸运的是,有统计和计算方法可以用来识别带噪声和复杂的数据中的模式。
相关性
一般来说,当我们谈到两个变量之间的「相关性(correlation)」时,在某种意义上,我们是指它们的「关系(relatedness)」。
相关变量是包含彼此信息的变量。两个变量的相关性越强,其中一个变量告诉我们的关于另一个变量的信息就越多。

你可能之前就看过:正相关、零相关、负相关
你可能已经对相关性、它的作用和它的局限性有了一定了解。事实上,这是一个数据科学的老生常谈:
「相关性不意味着因果关系」
这当然是正确的——有充分的理由说明,即使是两个变量之间有强相关性也不保证存在因果关系。观察到的相关性可能是由于隐藏的第三个变量的影响,或者完全是偶然的。
也就是说,相关性确实允许基于另一个变量来预测一个变量。有几种方法可以用来估计线性和非线性数据的相关性。我们来看看它们是如何工作的。
我们将用 Python 和 R 来进行数学和代码实现。本文示例的代码可以在这里找到:
GitHub https://gist.github.com/anonymous/fabecccf33f9c3feb568384f626a2c07
皮尔逊相关系数
皮尔逊相关系数(PCC, 或者 Pearson's r)是一种广泛使用的线性相关性的度量,它通常是很多初级统计课程的第一课。从数学角度讲,它被定义为「两个向量之间的协方差,通过它们标准差的乘积来归一化」。
两个成对的向量之间的协方差是它们在均值上下波动趋势的一种度量。也就是说,衡量一对向量是否倾向于在各自平均值的同侧或相反。

让我们看看在 Python 中的实现:
def mean(x):
return sum(x)/len(x)
def covariance(x,y):
calc = []
for i in range(len(x)):
xi = x[i] - mean(x)
yi = y[i] - mean(y)
calc.append(xi * yi)
return sum(calc)/(len(x) - 1)
a = [1,2,3,4,5] ; b = [5,4,3,2,1]
print(covariance(a,b))
协方差的计算方法是从每一对变量中减去各自的均值。然后,将这两个值相乘。
如果都高于(或都低于)均值,那么结果将是一个正数,因为正数 × 正数 = 正数;同样的,负数 × 负数 = 负数。
如果在均值的不同侧,那么结果将是一个负数(因为正数 × 负数 = 负数)。
一旦我们为每一对变量都计算出这些值,将它们加在一起,并除以 n-1,其中 n 是样本大小。这就是样本协方差。
如果这些变量都倾向于分布在各自均值的同一侧,协方差将是一个正数;反之,协方差将是一个负数。这种倾向越强,协方差的绝对值就越大。
如果不存在整体模式,那么协方差将会接近于零。这是因为正值和负值会相互抵消。
最初,协方差似乎是两个变量之间「关系」的充分度量。但是,请看下面的图:

协方差 = 0.00003
看起来变量之间有很强的关系,对吧?那为什么协方差这么小呢(大约是 0.00003)?
这里的关键是要认识到协方差是依赖于比例的。看一下 x 和 y 坐标轴——几乎所有的数据点都落在了 0.015 和 0.04 之间。协方差也将接近于零,因为它是通过从每个个体观察值中减去平均值来计算的。
为了获得更有意义的数字,归一化协方差是非常重要的。方法是将其除以两个向量标准差的乘积。