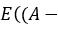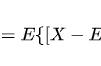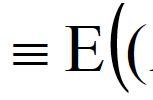在希腊字母中 ρ 常用来表示皮尔逊相关系数
在 Python 中:
import math
def stDev(x):
variance = 0
for i in x:
variance = (i - mean(x) ** 2) / len(x)
return math.sqrt(variance)
def Pearsons(x,y):
cov = covariance(x,y)
return cov / (stDev(x) * stDev(y))
这样做的原因是因为向量的标准差是是其方差的平方根。这意味着如果两个向量是相同的,那么将它们的标准差相乘就等于它们的方差。

有趣的是,两个相同向量的协方差也等于它们的方差。
因此,两个向量之间协方差的最大值等于它们标准差的乘积(当向量完全相关时会出现这种情况)。这将相关系数限制在 -1 到 1 之间。
箭头指向哪个方向?
顺便说一下,一个定义两个向量的 PCC 的更酷的方法来自线性代数。
首先,我们通过从向量各自的值中减去其均值的方法来「集中」向量。
a_centered = [i - mean(a) for i in a]
b_centered = [j - mean(b) for j in b]
现在,我们可以利用向量可以看做指向特定方向的「箭头」的事实。
例如,在 2-D 空间中,向量 [1,3] 可以代表一个沿 x 轴 1 个单位,沿 y 轴 3 个单位的箭头。同样,向量 [2,1] 可以代表一个沿 x 轴 2 个单位,沿 y 轴 1 个单位的箭头。

两个向量 (1,3) 和 (2,1) 如箭头所示。
类似地,我们可以将数据向量表示为 n 维空间中的箭头(尽管当 n > 3 时不能尝试可视化)。
这些箭头之间的角度 可以使用两个向量的点积来计算。定义为:

或者,在 Python 中:
def dotProduct(x,y):
calc = 0
calc = x[i] * y[i]
return calc
点积也可以被定义为: