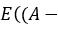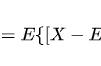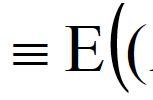上述公式中,加「^」表示「双中心」,加「-」表示「平均值」。
3. 在两个双中心矩阵的基础上,将 X 中每个元素的均值乘以 Y 中相应元素的均值,则可计算出距离协方差的平方。

4. 现在,我们可以用类似的办法找到「距离方差」。请记住,若两个向量相同,其协方差与其方差相等。因此,距离方差可表示如下:

5. 最后,我们利用上述公式计算距离相关性。请记住,(距离)标准差与(距离)方差的平方根相等。

如果你更喜欢代码实现而非数学符号,那么请看下面的 R 语言实现:
set.seed(1234)
doubleCenter <- function(x){
centered <- x
for(i in 1:dim(x)[1]){
for(j in 1:dim(x)[2]){
centered[i,j] <- x[i,j] - mean(x[i,]) - mean(x[,j]) mean(x)
}
}
return(centered)
}
distanceCovariance <- function(x,y){
N <- length(x)
distX <- as.matrix(dist(x))
distY <- as.matrix(dist(y))
centeredX <- doubleCenter(distX)
centeredY <- doubleCenter(distY)
calc <- sum(centeredX * centeredY)
return(sqrt(calc/(N^2)))
}
distanceVariance <- function(x){
return(distanceCovariance(x,x))
}
distanceCorrelation <- function(x,y){
cov <- distanceCovariance(x,y)
sd <- sqrt(distanceVariance(x)*distanceVariance(y))
return(cov/sd)
}
# Compare with Pearson's r
x <- -10:10
y <- x^2 rnorm(21,0,10)
cor(x,y) # --> 0.057
distanceCorrelation(x,y) # --> 0.509
任意两变量的距离相关性都在 0 和 1 之间。其中,0 代表两变量相互独立,而接近于 1 则表明变量间存在依赖关系。
如果你不想从头开始编写距离相关方法,你可以安装 R 语言的 energy 包(https://cran.r-project.org/web/packages/energy/index.html),设计此方案的研究者提供了本代码。在该程序包中,各类可用方案调用的是 C 语言编写的函数,因此有着很大的速度优势。
物理解释
关于距离相关性的表述,有着一个更令人惊讶的结果——它与布朗关联(Brownian correlation)有着确切的等价关系。
布朗关联指的是两个布朗过程之间的独立性(或依赖性)。相互依赖的布朗过程将会表现出彼此「跟随」的趋势。
让我们用一个简单的比喻来把握距离相关性的概念——请看下图中漂浮在湖面上的小纸船。
如果没有盛行风向,那么每艘船都将进行随机漂流——这与布朗运动类似。