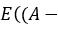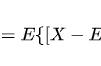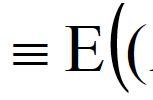无盛行风向时,小船随机漂流
如果存在盛行风向,那么小船漂流的方向将依赖于风的强度。风力越强,依赖性越显著。

有盛行风向时,小船倾向于同向漂流
与之类似,无关变量可以被看作无盛行风向时随机漂流的小船;相关变量可以被看作在盛行风向影响下漂流的小船。在这个比喻中,风的强弱就代表着两个变量之间相关性的强弱。
如果我们允许盛行风向在湖面的不同位置有所不同,那么我们就可以引入非线性的概念。距离相关性利用「小船」之间的距离推断盛行风的强度。

置信区间?
我们可以采取「重采样(resampling)」方法为距离相关性估计建立置信区间。一个简单的例子是 bootstrap 重采样。
这是一个巧妙的统计技巧,需要我们从原始数据集中随机抽样(替换)以「重建」数据。这个过程将重复多次(例如 1000 次),每次都计算感兴趣的统计量。
这将为我们感兴趣的统计量产生一系列不同的估计值。我们可以通过它们估计在给定置信水平下的上限和下限。
请看下面的 R 语言代码,它实现了简单的 bootstrap 函数:
bootstrap <- function(x,y,reps,alpha){
estimates <- c()
original <- data.frame(x,y)
N <- dim(original)[1]
for(i in 1:reps){
S <- original[sample(1:N, N, replace = TRUE),]
estimates <- append(estimates, distanceCorrelation(S$x, S$y))
}
u <- alpha/2 ; l <- 1-u
interval <- quantile(estimates, c(l, u))
return(2*(dcor(x,y)) - as.numeric(interval[1:2]))
}
# Use with 1000 reps and threshold alpha = 0.05
bootstrap(x,y,1000,0.05) # --> 0.237 to 0.546
如果你想建立统计显著性,还有另一个重采样技巧,名为「排列检验(permutation test)」。
排列检验与上述 bootstrap 方法略有不同。在排列检验中,我们保持一个向量不变,并通过重采样对另一个变量进行「洗牌」。这接近于零假设(null hypothesis)——即,在变量之间不存在依赖关系。
这个经「洗牌」打乱的变量将被用于计算它和常变量间的距离相关性。这个过程将被执行多次,然后,结果的分布将与实际距离相关性(从未被「洗牌」的数据中获得)相比较。
然后,大于或等于「实际」结果的经「洗牌」的结果的比例将被定为 P 值,并与给定的显著性阈值(如 0.05)进行比较。
以下是上述过程的代码实现:
permutationTest <- function(x,y,reps){
observed <- distanceCorrelation(x,y)
y_i <- sample(y, length(y), replace = T)
estimates <- append(estimates, distanceCorrelation(x, y_i))
}
p_value <- mean(estimates >= observed)
return(p_value)
}
# Use with 1000 reps
permutationTest(x,y,1000) # --> 0.036
最大信息系数
最大信息系数(MIC)于 2011 年提出,它是用于检测变量之间非线性相关性的最新方法。用于进行 MIC 计算的算法将信息论和概率的概念应用于连续型数据。
深入细节
由克劳德·香农于 20 世纪中叶开创的信息论是数学中一个引人注目的领域。
信息论中的一个关键概念是熵——这是一个衡量给定概率分布的不确定性的度量。概率分布描述了与特定事件相关的一系列给定结果的概率。

概率分布的熵是「每个可能结果的概率乘以其对数后的和」的负值
为了理解其工作原理,让我们比较下面两个概率分布: