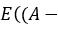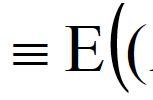也就是全体样本加上一个常数,整体的方差不变。如果我们的样本不是一个值,而是一个向量的话,那么这个公式可以拓展成样本加上一个常数向量,样本的方差保持不变。这个也很好理解,样本加上一个常数向量,相当于整体朝着向量的方向移动了一个距离,对于整体的分布并不会影响。
如果某个样本X的方差为0,那么说明样本内只有一个值。
下面一个性质稍微复杂一点:

也就是说方差等于样本平方的期望减去样本期望的平方,我们光从定义上很难得出这个结论,需要通过严谨的推导:

在有些时候,我们直接求解样本的方差不太方便,而求解平方的期望很容易,这个时候我们可以考虑使用这个公式进行代换。
方差与协方差方差我们一般不直接在机器学习当中进行使用,更多的时候是用在特征分析当中,查看特征的方差来感知它的离散情况,决定要不要对特征进行一些处理。因为对于一些模型来说,如果特征的方差过大,那么模型可能很难收敛,或者是收敛的效果可能会受到影响。这个时候往往需要考虑使用一些方法对特征值进行标准化处理。
除了方差之外,还有一个类似的概念也经常被用到,就是用来衡量两个变量之间相关性的协方差。
协方差的公式其实和方差也有脱不开的关系,我们先来简单推导一下。
首先,我们来看一下D(X Y),这里X和Y是两个变量,D(X Y)就表示X Y的方差,我们来看下D(X Y)和D(X)和D(Y)之间的关系。
我们可以来推导一下,根据方差的定义:

这里的N是一个常量,我们可以忽略,只用来看分子即可。我们把式子展开: