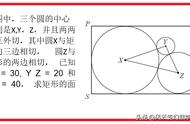
这是一道小学五年级数学题:长方形面积已知,求其对角线长!班上一个会的都没有,学霸也不例外!多数朋友认为,非超纲使用勾股定理不可!
如图一,

图一
长方形面积为40,由两个相同的小正方形组成,求对角线AB。
此题难点:①小学还没学勾股定理,无法使用。②简单勾股数也许有所介绍,但无法适用此题,因为其直角边长为无理数而非整数、分别为2√20和√20。
不用勾股定理或简单勾股数,该如何求解?唯一可能的办法只剩:拼图!
解析:
①将3个与直角三角形ABC相同的三角形AEF、EDG和DCH,与△ABC依序拼在一起。如图二

图二
②显然,ACDE为正方形。
③注意到,题意蕴含条件AB=2BC,故BF=AB-AF=AB-BC=BC。同理,可得BF=FG=GH=HB=BC。再由
∠AFE=∠DGE=∠DCH=∠CAB=90°,可知正方形ACDE的中心部分四边形BFGH为正方形。
④由对角线平分长方形面积可知,S△ABC=40÷2=20。
⑤由③知,图二中心小正方形与图一正方形相同。由图一可知,S小正方形=S△ABC=20。故S正方形ABDE=20×5=100。因此正方形ABDE的边长为10,也即AC=10。
—————————————————
友友们有好的思路或方法,欢迎留言分享!
,