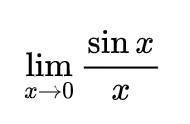应用洛必达法则解决恒成立问题的解题思路
解决恒成立问题的常用方法为分离变量法,通过参数与新函数的最值之间的关系求得结果.利用变量分离法处理时,会出现“(-∞,0]”型的代数式,而这是大学数学中的不定式问题,解决这类问题的有效方法就是利用洛必达法则.
考点2确定分类讨论标准
应用洛必达法则确定分类讨论标准
注意应用洛必达法则解决的试题应满足:
(1)可以分离变量;
(2)用导数可以确定分离变量后一端新函数的单调性;
(3)出现“”型未定式.
数学建模
1.【解读素养】数学建模是对现实问题进行数学抽象,用数学语言表达问题、用数学方法构建模型解决问题的素养.数学建模过程主要包括:在实际情境中从数学的视角发现问题、提出问题,分析问题、建立模型,确定参数、计算求解,检验结果、改进模型,最终解决问题.

【素养落地】解决恒成立,不等式,求参数范围等问题时,运用参数分离是一种基本思路,但新函数,常常无法运用导数确定函数单调性.运用洛必达法则,可解决(-∞,0]型未定式问题.充分考查了学生观察、联想、转化与划归思想,是数学建模素养核心素养的集中表现.
参考答案: