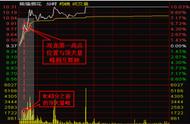
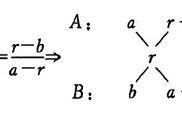十字交叉法是理科中一个应用比较广泛的重要的方法,数学、化学、物理等学科都会用到十字交叉法,但很多人又只是听说过,却不能熟练运用,很好的运用十字交叉法,有助于快速准确的解决数学问题。那么,我们小学数学如何运用到十字交叉法呢?
题型一:比较分数的大小
我们知道在分数的比较中,同分母分数,分子大的分数值大;同分子分数,分母小的分数值大;异分母分数则要把分母化为同分母分数才能进行比较。在教学中,我发现让学生记住这几条并不难,可是却非常容易混淆,或者是根本就不会运用。但是如果运用十字交叉相乘法,学生不但都能很快的得出答案,而且不管什么分数间进行比较都能够通用。

注:所得的积必须写在分数线上方(即作为新分子)。
从上例很明显可以看出,十字交叉法比较两分数的大小的实质上就是通分。不过,却省去了学生对分数进行通分的过程和时间,从而一步到位,更简单更直接,只要会乘法的学生,在比较分数之间的大小时基本上都不费吹灰之力了。
题型二:解比例
很多老师和学生都知道,解比例的依据是比例的基本性质,即在比例中,两个内项的积等于两个外项的积。可当比例变化为a/b=c/d(a≠0,c≠0)这种形式时,有些学生便找不着内外项了,或者有某些学生还要把上式化为a:b=c:d(a≠0,c≠0)的形式,这就走了弯路,浪费了时间不说而且变换后也很容易出错。

可见,利用此方法既直观又便于记忆,而且在较复杂的比例中,更能体现出些法的简便性与适用性,由于篇幅有限,在此就不一一介绍了。
题型三:解归一问题或正比例问题
其实正比例问题也就是归一问题,此类应用题中暗含着单一量不变,文字叙述中多带有类似“照这样计算”的字样,其解题的关键是从已知的一种对应量中求出单一量(即归一),再以它为标准,根据题目要求算出所求量。
这种解法主要是有时候有的学生找不到到底怎样去求出单一量(也就是标准量),如果找不到标准量,那么对于这类问题学生就无法进行求解。若是采用十字交叉相乘法设未知数进行列方程求解,此类问题就会变得简单明了。
例3:小明10分钟走750米,照这样计算,从学校到家小明需要走24分钟,从学校到小明家的路程有多少米?
解析:
方法一:先根据 速度=路程÷时间 算出小明的速度,再根据 路程=速度×时间 计算出学校到小明家的路程。
750÷10=75(米/分钟)
75×24=1800(米)
方法二:用正比例的知识解。
解:设从学校到小明家的路程有x米。
750:10=x:24
x=750×24÷10
x=1800
方法三:先找出题中所有的量出来
时间(分钟)
路程(米)
①
10
750
②
24
x
注:必须要单位对应。
解:设从学校到小明家的路程有x米。
10x=750×24
x=1800
答:从学校到小明家的路程有1800米。
题型四:浓度问题
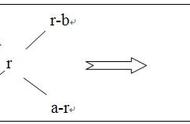
如果题目中给出两个平行的情况A, B, 满足条件a, b ; 然后A和B按照某种条件混合在一起形成的情况C, 满足条件c. 而且可以表示成如下的表达式. 那么这个时候就可以用十字交叉法。
判断式:A×a B×b=(A B)×c=C×c

(一)基本知识点:
1、溶液=溶质 溶剂; 2、浓度=溶质/溶液; 3、溶质=溶液*浓度; 4、溶液=溶质/浓度;
(二)例题与解析
1、甲容器中有浓度为4%的盐水250克,乙容器中有某种浓度的盐水若干克。现从乙中取出750 克盐水,放人甲容器中混合成浓度为8%的盐水。问乙容器中的盐水浓度约是多少?
A.9.78% B.10.14% C.9.33% D.11.27%
答案:C
解析:
方法一:设乙容器中盐水的浓度为x
(250×4%+750*x)/(250+750)=8%
x=9.33%
方法二:设浓度为x