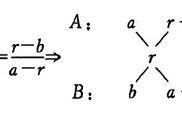今天想和大家分享的是十字交叉法,这个方法应用范围极广,它本身属于方程法的一种变形,只是形式上不同而已,本质就是方程法,所以大家可以放心使用。
接下来请大家记住它的形式:部分放在左边的上方与下方,整体放中间,十字交叉作差,大数减小数,最终结果之比根据题目有所不同。具体来说:当该问题属于平均数问题,十字交叉之后的比例为总数之比;当当该问题属于增长率问题,十字交叉之后的比例为基期量之比;当该问题属于利润率问题,十字交叉之后的比例为成本之比;当该问题属于浓度问题,十字交叉之后的比例为溶液之比;当该问题属于折扣问题,十字交叉之后的比例为原价之比。形式总体如下:

以平均数问题为例,其中,A代表A班或A单位人数,a代表A班平均数;B代表B班或B单位总人数,b代表B班平均数;r代表的是A班与B班混合后整体的平均数,(假设a>b),最终我们就可以求出其中的未知量,以上所有的类型可通用,下面还是以具体题目带大家感受下:
【例】某单位共有职工72人,年底考核平均分数为85分,根据考核分数,90分以上的职工评为优秀职工,已知优秀职工的平均分为92分,其他职工的平均分数是80分,问优秀职工的人数是多少人:
A.12 B.24
C.30 D.42
其实我们用方程完全可以做出来,但是比较耗时。我们来分析这道题,有整体平均数,有两个部分平均数,完全可以知道两个部分人数之比,又知道总人数,即可以求出部分的人数。接下来我们用十字交叉来处理:

所以优秀职工与其他职工人数之比为5:7,单位总共有72人,分为12份,优秀职工占5份,故有30人。因此,选择C选项。
【例2】学校体育部采购一批足球和篮球,足球和篮球的定价分别为每个80元和100元。由于购买数量较多,商店分别给予足球25%、篮球20%的折扣,结果共少付了22%。问购买的足球和篮球的数量之比是多少?
A.4:5 B.5:6
C.6:5 D.5:4
观察这道题目,给出的是总体的折扣以及两个部分的折扣,根据十字交叉可求出两个部分的原价之比,因为知道单价,所以数量很容易解出。

可知足球和篮球原价之比为2:3,又因为足球和篮球单价之比为80:100=4:5,所以数量之比为5:6。因此,选择B选项。
类似的题目还有非常多,如果大家感兴趣的话我们可以持续关注,关注人数较多的话我们继续为大家分享其他类型的题目。

更多备考资料: