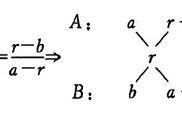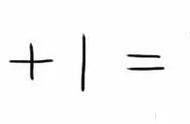一些朋友常常被十字交叉法搞懵,首当其冲的是溶液问题,今天通过这篇帖子我们彻底告别十字交叉的烦恼。
十字交叉最初是很传统的推导:
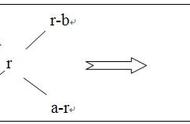
若有两种质量分别为 A 与 B 的溶液,其浓度分别为 a 与 b,混合后浓度为 r,则由溶质质量不变可列出下式 Aa Bb=(A B)r,对上式进行变形可得
A/B=r-b/a-r,在解题过程中一般将此式转换成如下形式:

需要注意的是:得到的比例是基础的比例(混合前的),基数什么内容,比例是什么内容。十字交叉可以应用在浓度混合、比重、人口、平均分等问题中,这些问题列方程有一个共性:即 Aa Bb=(A B)r。
然而,近些年,十字交叉法基本不会再以简单形式来考察,为提升难度,多在复杂的题目、多次混合、融合问题、结合比例、概念理解等方式命题,我们通过例题来看十字交叉的逐步升级。
一、典型例题:公务员考试较少,选调、事业、村官等还是有的。
例1:某班全部同学平均身高1.63米,其中男生平均身高1.71米,女生平均身高1.61米。该班女生所占比例约为( )(湖南选调生真题)
A.20% B.25% C.75% D.80%
解析:D。男/女=(1.63-1.61)/(1.71-1.63)=1/4,即女/(男 女)=4/(1 4)=80%
例2:车间40人,技术考核平均分80分,男生平均分83,女生平均分78,问女生多少人?
A.16 B.18 C.20 D.24
解析:D。女/男=(83-80)/(80-78)=3/2,即女/整体=3/5,女=40×3/5=24。
例3:某市现有70万人口,如果5年后城镇人口增加4%,农村人口增加5.4%,则全市人口将增加4.8%,那么这个市现有城镇人口:(资料分析真题)
A 30万 B 31.2 万 C 40万 D 41.6万
解析:A。城/农=(5.4-4.8)/(4.8-4)=6/8=3/4,城=3/7×70=30。
二、多次混合:还是比较简单的题型,混合几次,则使用几次十字交叉。
例4、某单位共有A.B.C.三个部门,三部门人员平均年龄分别为38岁,24岁,42岁,A和B两部门人员平均年龄为30岁,B和C两部门平均年龄为34岁,该单位全体人员平均年龄为多少岁?
A34 B35 C36 D37
解析:B。
AB混合: BC混合:
38 6 24 8
30 34
24 8 42 10
即A:B:C=6:8:10=3:4:5,则全体平均=(38×3 24×4 42×5)/(3 4 5)=(19 16 35)/2=35。这个题比例是统一的,不同的比例也可以根据相同一项来统一。
例5、某单位有2个处室,甲处室有12人,乙处室有20人。现在将甲处室最年轻的4人调入乙处室,则乙处室的平均年龄增加了1岁,甲处室的平均年龄增加了3岁。问在调动之前,两个处室的平均年龄相差多少岁( )
A.8 B.12 C.14 D.15
解析:B。
浓度混合问题1:十字相乘法。混合两次,要用两次十字相乘。假设甲人平均A,乙平均B,4人平均C。
4人与乙混合/人数 4人与甲去除4人混合/人数
C 1 4 A 3 A-C 8
B 1 A
B C-B-1 20 C 3 4
得出 C-B-1=5 即C=B 6A-C=6 即A=C 6
得出A=B 12。甲平均数是A,是不是甲去除4人再与这4人混合平均数还是A。
三、题目复杂:看透复杂的形势,找到本质—公务员的必备素质。
例6、某高校艺术学院分音乐系和美术系两个系别,已知学院男生人数占总人数的30%,且音乐系的男女生人数之比为1:3,美术系男女生人数之比为2:3,问音乐系和美术系的总人数之比为多少?( )
A.5:2 B.5:1 C.3:1 D.2:1
解析:D。这个的确是十字交叉。将比例转化为百分数,音乐系男占25%,美术系男占40%,仅仅是一个等价变换,就明显了。音乐/美术=(40-30)/(30-25)=10:5=2:1。(这个题也属于结合比例的题)
解析:A。
红黑总价各优惠 红黑混合优惠 红黑总价格
85 2
100-18=82
80 3
红色数量:黑色数量=2/5:3/9=6:5,则红色=66×6/11=36。
解析:D。
增长率 混合增长率 混合前基数(基期)
10 7
18
25 8
问题是2017年的即现期的产量比,2017年的=2016年基期×同比增长率,即7(1 10%):8(1 25%)=7.7:10。
最后注意,十字交叉法不是思考分析的方法,而是简化了计算的过程,在分秒必争的行测中非常重要,朋友可以找专项题目刷题,套用我的思路,很快就可以拿下了。