#公因子数设为2个,拟合
fa_5 = FactorAnalyzer(rotation=None, n_factors=2, method='principal')
fa_5.fit(df_features)
#查看公因子提取度
print("\n公因子提取度:\n",fa_5.get_communalities())
#查看因子载荷
print("\n因子载荷矩阵(未旋转):\n",fa_5.loadings_)
公因子提取度:
[0.5615 0.4024 0.2833 0.4777 0.6124 0.5424 0.2845 0.3844]
因子载荷矩阵(未旋转):
[[ 0.5277 0.532 ] [ 0.3946 0.4966]
[ 0.3625 0.3898] [ 0.4562 0.5192]
[ 0.5995 -0.5031] [ 0.6017 -0.4246]
[ 0.4426 -0.2977] [ 0.5376 -0.3088]]
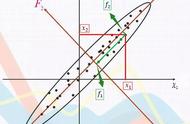
旋转提取因子很多时候我们从因子载荷矩阵中很难去解释主成分所蕴含的逻辑关系,因此就需要将因子载荷矩阵进行旋转。
旋转的目的是通过改变坐标轴位置,重新分配各个因子所解释方差比例,使其载荷系数更接近1或0,能更好地解释和命名变量。旋转后的因子不改变模型对数据的拟合程度,也不改变各个变量的公因子方差,使因子结构变得更简单。
假如我们使用varimax方法旋转后,还是不能很好地解释主成分所蕴含的逻辑,那么我们就需要用其它旋转方法进行探索,这里以promax进行展示。
#使用最大方差法旋转因子载荷矩阵
fa_5_rotate = FactorAnalyzer(rotation='varimax', n_factors=2, method='principal')
fa_5_rotate.fit(df_features)
#查看旋转后的因子载荷
print("\n旋转后的因子载荷矩阵(有旋转):\n\n",fa_5_rotate.loadings_)
print("因子载荷矩阵(有旋转):\n")
loadings = pd.DataFrame(data= fa_5_rotate.loadings_.round(3),columns=['F1','F2'],index=df_features.columns)
loadings:因子载荷矩阵
V1~V8:可以用因子载荷矩阵对应值线性表出。
如:V1=0.091*F1 0.744*F2,其他变量同理。

# 因子得分系数阵(等于相关系数矩阵的逆乘以因子载荷矩阵)
X1 = np.mat(df_corr)
X1 = nlg.inv(X1)
factor_score = np.dot(X1,fa_5_rotate.ladings_)
factor_score = pd.DataFrame(factor_score)
factor_score.columns = ['factor1', 'factor2']
factor_score.index = df_corr.columns
print("\n因子得分系数阵:\n", factor_score)
*因子系数阵的因子可以被变量线性表出。
如:factor=-0.028069*V1-0.063343*V2-0.029759*V3-0.049737*V4 0.442872*V5 0.410131*V6 0.295427*V7 0.336172*V8
在此系数阵的每一行中找出绝对值最大的值。显然能形成两大类。