F_score = np.dot(np.mat(df_features), np.mat(factor_score))
print("\n2个因子得分:\n",pd.DataFrame(F_score))

#取方差值,作为计算综合分的权重
weight_var = fa_15_sd[1][0:2]
weight_var2 = np.mat(weight_var).T
#计算综合分zh
total_score = np.dot(F_score,weight_var2)
zh = pd.DataFrame(total_score,index=df_features.index)
zh.columns=['zh']
F = pd.DataFrame(F_score,index=df_features.index)
F.columns={'F1','F2'}
#连接数据集
totall_zh = df_features.join([F,zh])

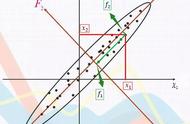
(1)降维。把原数据集8个变量V1~V8表示的信息降维到F1,F2两个变量表出。如果是100个变量呢?同样可以降低维度,降低分析问题的复杂度。
(2)发现潜在因素。该案例中找出了两个因素,factor1和factor2,可以用于概括数据集所隐含的本源涵义。为结构方程模型分析做基础。
(3)zh可以用来量化评价每个样本。把本由多指标度量的问题化简为用一个综合指标来代替。便于排序(排名次)。
(4)本案例原数据集变量用字母V1~V8表示,并没给出每个变量的明确的经济意义或者具体的指标名称。可能是“每股收益”,也可能是“存货周转率”,亦可能是“考试成绩”等。(财务管理中所讲到的:净资产收益率 总资产报酬率 速动比率 流动比率 存货周转率 应收账款周转率 总资产增长率 销售利润率 资产负债率),大家可以据此思路再做扩展。