第五单元 圆
一、圆的特征
1. 圆是由一条曲线围成的封闭的平面图形。
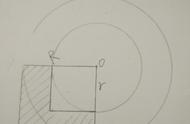
2. 圆心o:圆中心的一点叫做圆心.
半径r:连接圆心到圆上任意一点的线段叫做半径。
直径d: 通过圆心且两端都在圆上的线段叫做直径。
3. 在同一个圆里,有无数条半径,也有无数条直径,所有的半径都相等,所有的直径都相等,直径是圆内最长的线段。圆心确定圆的位置,半径确定圆的大小。
4. 在同圆或等圆内直径是半径的2倍,半径是直径的一半:d=2r 或 r=d/2。
5. 圆是轴对称图形:直径所在的直线是圆的对称轴,圆、圆环有无数条对称轴。
半圆、扇形只有一条对称轴。
- 圆的周长:
1.围成圆的曲线的长度叫做圆的周长,周长用字母C表示。
2. 圆周率:圆的周长与直径的比值是一个固定的数,叫做圆周率,用字母π表示。
圆的周长=直径×圆周率 c=πd, c=2πr d=c÷π r=c÷π÷2
注:圆周率π是一个无限不循环小数,3.14是近似值。
3. 周长的变化的规律:半径扩大多少倍,直径也扩大多少倍,周长扩大的倍数与半径、直径扩大的倍数相同。
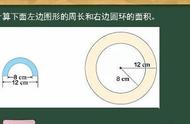
4. 半圆周长 = 圆周长一半 直径 =1/2×2πr d = πr d = πr 2r
- 圆的面积
1. 圆面积公式 :S圆 = πr2 S半圆 =1/2πr2
2. 几种图形,在面积相等的情况下,圆的周长最短,而长方形的周长最长;反之,在周长相等的情况下,圆的面积则最大,而长方形的面积则最小。
3. 圆面积的变化的规律:半径扩大多少倍,直径、周长也同时扩大多少倍,而圆面积扩大的倍数是半径、直径扩大的倍数的平方倍。
4. 环形面积 = 大圆的面积 – 小圆的面积=πR2 - πr2=π(R2 - r2)
扇形面积 = πr2×n/360(n表示扇形圆心角的度数)
5. 跑道:每条跑道的周长等于两半圆跑道合成的圆的周长加上两条直跑道的和。因为两条直跑道长度相等,所以,起跑线不同,相邻两条跑道起跑线也不同,间隔的距离是:2×π×跑道宽度。
注:一个圆的半径增加a厘米,周长就增加2πa厘米
一个圆的直径增加b厘米,周长就增加πb 厘米。
6. 常用数据:1π=3.14 2π=6.28 3π=9.42 4π=12.56 5π=15.7
6π=18.84 7π=21.98 8π=25.12 9π=28.26 112=121 122=144 132=169 142=196 152=225 162=256 172=289 182=324 192=361
第六单元、百分数
- 百分数的意义:表示一个数是另一个数的百分之几。
注:百分数是专门用来表示一种特殊的倍比关系的,表示两个数的比,所以,百分数又叫百分率或百分比。百分数的计量单位是1%,百分数后面不能带单位名称。
1. 百分数和分数的区别和*
(1)*都可以用来表示两个量的倍比关系。
(2)区别:意义不同:百分数只表示倍比关系,不表示具体数量,所以不能带单位名称。分数不仅表示倍比关系,还能带单位表示具体数量。
百分数的分子可以是小数,分数的分子只能是整数。
2. 小数、分数、百分数之间的互化
(1)百分数化小数:小数点向左移动两位,去掉“%”。
(2)小数化百分数:小数点向右移动两位,添上“%”。
(3)百分数化分数:先把百分数改写成分母是100的分数,然后化成最简分数。
(4)分数化百分数:分子除以分母得到小数,再把小数化成百分数。
(5)小数化分数:把小数化成分母是10、100、1000等的分数再化简。
(6)分数化小数:分子除以分母。
二、百分数应用题
1. 求一个数是另一个数的百分之几?用:一个数÷另一个数
2. 求一个数比另一个数多(或少)百分之几?用:(大数-小数)÷单位“1”的量。
(1)求甲比乙多百分之几?用(甲-乙)÷乙
(2)求乙比甲少百分之几?用(甲-乙)÷甲
3. 求一个数的百分之几是多少 ?用:一个数(单位“1”) ×百分率
4. 已知一个数的百分之几是多少,求这个数。用:部分量÷百分率=一个数(单位“1”)
5. 折扣、打折的意义:几折就是十分之几也就是百分之几十。
第七单元、统计
1. 扇形统计图的意义:用整个圆的面积表示总数,用圆内各个扇形面积表示各部分数量同总数之间关系,也就是各部分数量占总数的百分比,因此也叫百分比图。
2. 常用统计图的优点:
(1)条形统计图直观显示每个数量的多少。
(2)折线统计图不但能看出各个数量的多少,而且还可以清楚地看出数量的增减变化情况。
(3)扇形统计图直观显示部分和总量的关系。