当古希腊人发现地球是球形以后,天文学家对宇宙模型的研究才真正开始。模型的基本原件就是地球、太阳、月亮、五大行星和恒星天球,天文学家的任务就是怎样“摆弄”这几个元件,构建起他们的模型,看看能否合理地解释我们看到的种种天象,尤其是要对行星的顺、逆、留等怪异行踪作出合理的解释,看看能否凭借模型预测天体在任何时刻的位置。
从公元前5世纪开始,古希腊天文学家提出了多种宇宙模型,如菲洛劳斯的中央火模型、欧多克斯的太阳运动模型……

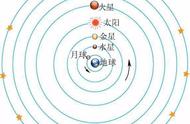
中央火模型认为宇宙中心是一团火,地球、月亮、太阳都自西向东绕着中央火旋转,最外面的恒星天球是静止的。
这些模型都只对天体的运动做了简单的描述,没有使用代数进行定量分析。就好比“人类是怎么起源的?”这个问题,在没有掌握足够证据之前,你可以提出无数种说法,比如上帝创造了人类,女娲捏土造人、外星移民……
直到公元前336-公元前323年,亚历山大大帝统一古希腊、古埃及、巴比伦,建立起庞大的帝国,把古希腊的几何天文学带到巴比伦的算术天文学面前,两者的结合诞生了卓有成效的希腊化天文学。从这时开始,才有人将数学推理计算作为支撑,放入到天体运行模型中。这其中的代表人物是阿里斯塔克、埃拉托斯尼、托勒密。阿里斯塔克计算出太阳远大于地球,并由此提出了日心说;埃拉托斯尼计算出地球周长;托勒密提出独霸千年的地心说。
为什么古希腊天文学需要借助巴比伦的代数,才能取得这么大的成就?这就要从毕达哥拉斯说起了。最开始古希腊人研究数学有2个方向:代数、几何学。后来毕达哥拉斯及其学派发现勾股定理,并进而发现了无理数,导致了第一次数学危机。于是古希腊人就将研究方向转向了几何学,这就导致古希腊人的代数水平相对较差,落后于巴比伦人。
当古希腊众多的天文学家正在冥思苦想日月星辰究竟是如何围绕地球旋转的时候,阿里斯塔克竟然大胆地提出,地球是围绕太阳旋转的,这真可谓是石破天惊。对于他的生平事迹,我们知道的很少,他大约生活在公元前310年至公元前230年之间。他写过一篇《论日月的大小和距离》的专论,向我们展示了希腊几何演绎推理的威力。
《论日月的大小和距离》文章开篇首先提出6条假设:
1、月球的光来自太阳;
2、地球位于一球体中心,月球在该球上运动;
3、当月亮上下弦时,将月球分为明暗两部分的大圆和我们的视线在同一平面上;
4、当月亮上下弦时,月球与太阳之间的角距离比一个直角小其1/30;
5、地球阴影的宽度为月球直径的2倍;
6、月球的视角直径相当于黄道上一宫的1/15。
然后运用平面几何的基本原理,证明了18个命题,其中包含了以下3个结论性的命题:
1、太阳和地球间的距离大于地球到月球距离的18倍,但小于其20倍;
2、太阳与月球的直径比大于18,但小于20;
3、地球与太阳的直径之比大于19比3,但小于43比6。
下面让我们一起来看看他是如何得出这些结论的。
前面2条假设很好理解,说的是月球围绕地球做圆周运动,月球的光来自太阳。
假设3“当月亮上下弦时,将月亮分为明暗两部分的大圆和我们的视线在同一平面上”,我们可以通过一个模型进行说明。

月相变化原理图

如下图图所示,如果有一个圆球,在平行光束的照射下,一半亮,另一半暗,那么用一个假想的平面S在圆球的明暗分界线插入,平面S与平行线光束必然相垂直。所以平面上的任一点处向圆球的中心看去,该视线与平行光束垂直。