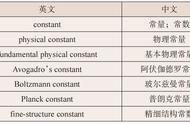
毕达哥拉斯常数
没错,就是那个引发第一次数学危机的数字——√2 ≈ 1.4142135623730950488。

公元前500年,有一位牛人,叫毕达哥拉斯。如果你对这位牛人有点儿陌生,那毕达哥拉斯定理应该知道吧,那就是:直角三角形中,两直角边的平方和等于斜边的平方。
在中国,这被称为“勾股定理”。
他创办了一个数学学派,叫做毕达哥拉斯学派,该学派认为:整数就像原子一样,构成了宇宙中的一切,并可以描述宇宙中的一切。宇宙间各种关系都可以用整数或整数之比来表达,除此之外,就什么都没有了。。。

而毕达哥拉斯的弟子——希勃索斯,在研究老师的定理时,发现了一个神奇的现象:边长为1的正方形,其对角线的长竟然无法用整数或整数之比表示出来!
于是,他把这个惊人的发现告诉了老师毕达哥拉斯。。。

希勃索斯本来以为老师会将这一发现公布于众,改变人们错误的认识。
没想到,老师却认为这样会动摇到毕达哥拉斯学派在学术界的统治地位,便新规定了一条纪律:谁都不准泄露存在根号2(即无理数)的秘密。
后来,天真的希勃索斯有一次无意中向别人谈到了他的发现,结果他被认为是学派的“逆贼”,被囚禁,受尽百般折磨,最后被投入爱琴海淹死。。。
关于希勃索斯的死有很多个版本,众说纷纭,但无论如何,希勃索斯都被人们当作是发现无理数的第一人。
√2就是第一个被发现的无理数,它的应用非常广泛,比如我们平常用的A4纸长宽之比就等于√2。