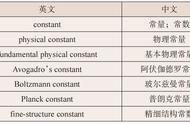
表示。

不过,对于这个神秘的常数,人们了解的还是很少,除了它的精确值不容易求出之外,关于辛钦常数是否为无理数,到目前也还没有人能证明。
圆周率π
圆周率 π ≈ 3.14159是圆的周长与直径的比值,是精确计算圆周长、圆面积、球体积等几何形状的关键值,人类很早就认识到了圆周率的存在。
公元前3世纪初,欧几里得在其著作《几何原本》中就提到过圆周率是常数;公元前2世纪左右,中国古算书《周髀算经》中有“径一而周三”的记载,也认为圆周率是常数。
而如今用来表示圆周率的希腊字母π,本来与圆周率毫无关系,只是从1736年开始,欧拉在书信和论文中都用π来表示圆周率,久而久之,人们就普遍认同π就是圆周率了。

π应该是数学中最基本、最重要、最神奇的常数了,人类对它的探索就从来没停止过,不过,从它的出现到确定它是无理数,人类就花了3000年的时间。。。
直到1761年,德国数学家朗伯(Lambert)才证明了 π 是一个无理数。
1882 年,德国数学家林德曼(Ferdinand von Lindemann)证明了圆周率 π 是一个超越数。(不满足任一个整系数代数方程的数)
自然底数e

17世纪末,伯努利(Bernoulli)发现了一个有趣的现象,